In the ever-evolving landscape of deep learning, Multi-Layer Perceptrons (MLPs) have long reigned supreme as the go-to architecture for approximating non-linear functions. However, despite their prevalence, MLPs come with limitations, particularly in terms of accuracy and interpretability. This is where Kolmogorov-Arnold Networks (KANs) step in, offering a compelling alternative inspired by a powerful mathematical theorem.
The Inspiration: Kolmogorov-Arnold Representation Theorem
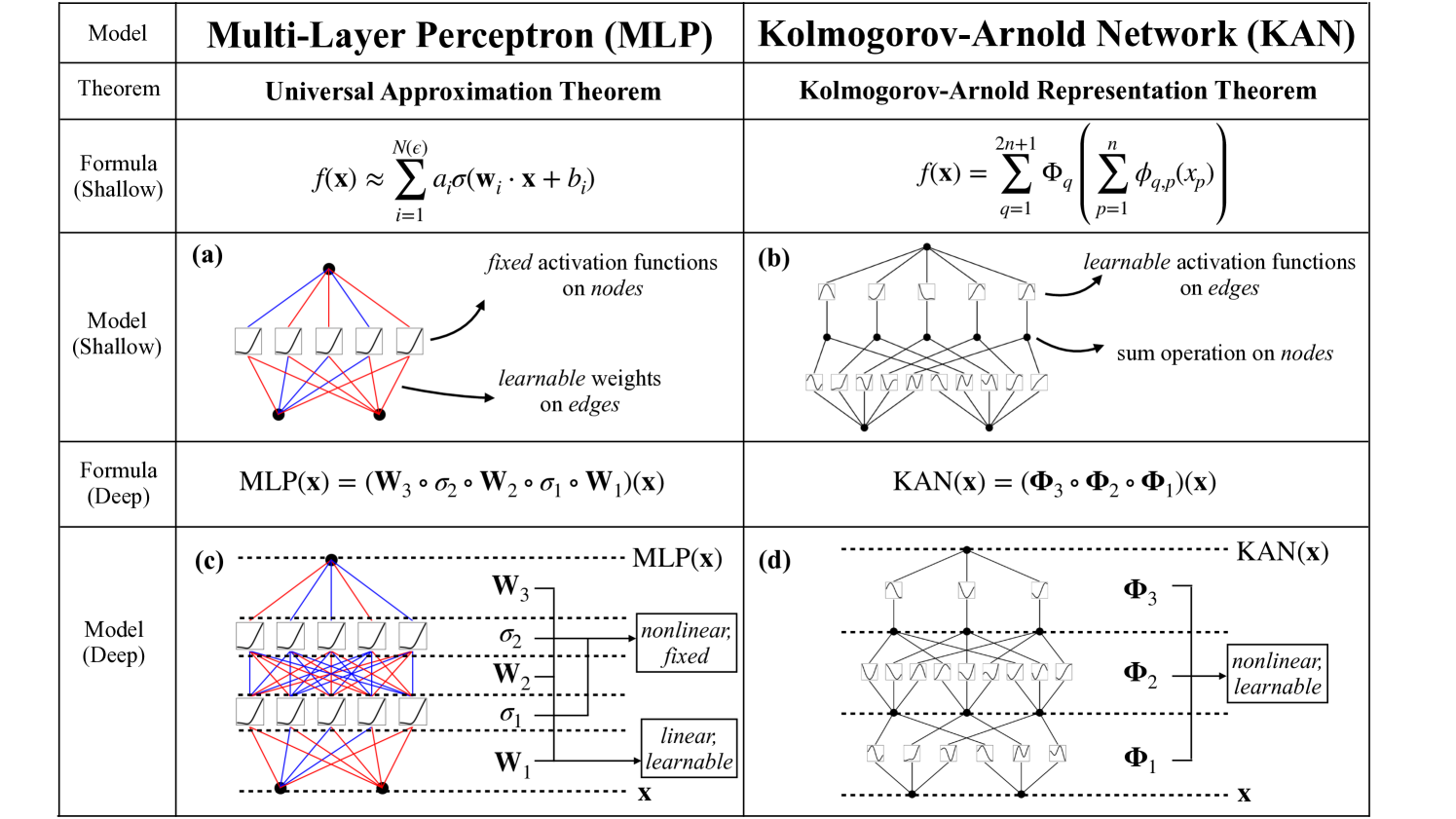
KANs draw their inspiration from the Kolmogorov-Arnold Representation Theorem, which states that any continuous multivariate function can be expressed as a composition of single-variable functions and addition. This essentially means that the complexity of a high-dimensional function can be broken down into simpler, one-dimensional components.
KAN Architecture: Learnable Activation Functions on Edges
Unlike MLPs, which employ fixed activation functions on nodes (“neurons”), KANs place learnable activation functions on edges (“weights”). These activation functions are typically parameterized as splines, allowing for greater flexibility and accuracy in approximating complex functions. As a result, KANs eliminate the need for linear weight matrices altogether.
Advantages of KANs: Accuracy and Interpretability
KANs offer several key advantages over MLPs:
- Accuracy: KANs can achieve comparable or even superior accuracy compared to MLPs, despite having smaller network sizes. This is due to their ability to efficiently learn both the compositional structure and the individual univariate functions of a given problem.
- Interpretability: The visualization of KANs is intuitive and user-friendly. By analyzing the activation functions on the edges, we can gain insights into the inner workings of the network and understand how it arrives at its predictions.
- Interactivity: KANs can be easily interacted with and modified by users. Through techniques like sparsification, pruning, and symbolization, users can simplify the network and extract meaningful symbolic representations of the learned functions.
- Scientific Discovery: KANs can serve as valuable tools for scientific exploration, aiding researchers in discovering mathematical relationships and physical laws. Examples include uncovering connections between knot invariants in mathematics and identifying phase transition boundaries in physics.
Overcoming the Curse of Dimensionality
One of the most significant challenges in machine learning is the curse of dimensionality, where the performance of models deteriorates as the number of input variables increases. KANs, due to their ability to decompose high-dimensional functions into lower-dimensional components, can effectively mitigate this issue and achieve favorable scaling laws compared to MLPs.
Continual Learning with Local Plasticity
KANs exhibit local plasticity, meaning that updates to the network primarily affect specific regions responsible for relevant skills, leaving other areas untouched. This characteristic allows KANs to excel in continual learning scenarios, where they can learn new tasks without forgetting previously acquired knowledge, a common problem faced by MLPs.
Applications of KANs: A Glimpse into the Future
The potential applications of KANs are vast and varied. From data fitting and PDE solving to scientific discovery and even image representation, KANs are poised to play a crucial role in advancing various fields. Their ability to learn and represent complex functions accurately and interpretably opens doors for more efficient and insightful deep learning models.
KANs: A New Language for AI + Science Collaboration
KANs can be seen as a “language model” for scientific exploration, allowing AI and human researchers to communicate and collaborate using the language of functions. This collaborative approach can lead to new scientific breakthroughs, with AI assisting scientists in uncovering hidden patterns and formulating new hypotheses.
Choosing between KANs and MLPs: A Decision Guide
While KANs offer several advantages, their training can be slower compared to MLPs. The choice between these architectures depends on the specific requirements of the task at hand. If interpretability and accuracy are paramount, and training time is not a major concern, KANs can be a powerful tool. However, if fast training is crucial, MLPs may be the preferred choice.
In conclusion, Kolmogorov-Arnold Networks present a promising alternative to traditional MLPs, offering enhanced accuracy, interpretability, and interactivity. As research in this area continues, we can expect to see KANs playing a significant role in shaping the future of deep learning and AI-powered scientific discovery.
Ref
https://arxiv.org/html/2404.19756v1