The State Space Model taking on Transformers

Right now, AI is eating the world.
And by AI, I mean Transformers. Practically all the big breakthroughs in AI over the last few years are due to Transformers.
Mamba , however, is one of an alternative class of models called State Space Models ( SSMs ). Importantly, for the first time, Mamba promises similar performance (and crucially similar scaling laws) as the Transformer whilst being feasible at long sequence lengths (say 1 million tokens). We achieve this long context by removing the “quadratic bottleneck” in the Attention Mechanism. Mamba also runs fast – like “up to 5x faster than Transformer fast”.
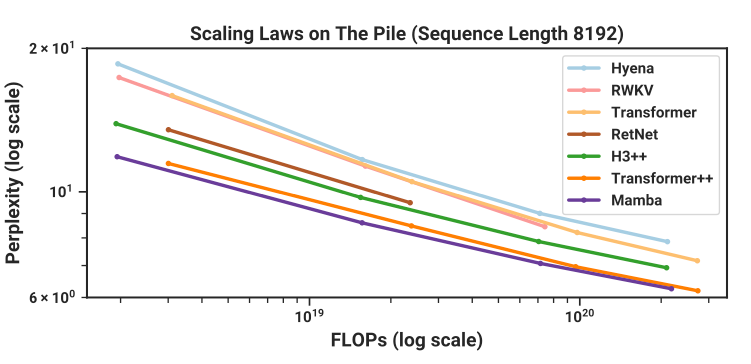
Mamba performs similarly (or slightly better than) other Language Models on The Pile
Gu and Dao, the Mamba authors write:
Mamba enjoys fast inference and linear scaling in sequence length, and its performance improves on real data up to million-length sequences. As a general sequence model backbone, Mamba achieves state-of-the-art performance across several modalities such as language, audio, and genomics. On language modeling, our Mamba-3B model outperforms Transformers of the same size and matches Transformers twice its size, both in pretraining and downstream evaluation.
Here we’ll discuss:
- The advantages (and disadvantages) of Mamba (🐍) vs Transformers (🤖),
- Analogies and intuitions for thinking about Mamba, and
- What Mamba means for Interpretability, AI Safety and Applications.
Problems with Transformers – Maybe Attention Isn’t All You Need
We’re very much in the Transformer-era of history. ML used to be about detecting cats and dogs. Now, with Transformers, we’re generating human-like poetry, coding better than the median competitive programmer, and solving the protein folding problem.
But Transformers have one core problem. In a transformer, every token can look back at every previous token when making predictions. For this lookback, we cache detailed information about each token in the so-called KV cache.

When using the Attention Mechanism, information from all previous tokens can be passed to the current token
This pairwise communication means a forward pass is O(n²) time complexity in training (the dreaded quadratic bottleneck) and each new token generated autoregressively takes O(n) time. That is to say, as the context gets larger, the model gets slower.
To add insult to injury, storing this KV cache requires O(n) space. The fateful CUDA OOM error looms large as the memory footprint balloons. If space were the only issue, we might just add more GPUs but with latency growing quadratically… perhaps not.
On the margin, we can mitigate the quadratic bottleneck with techniques like Sliding Window Attention or clever CUDA optimisations like FlashAttention. But ultimately, for super long context windows (like a chatbot which remembers every conversation you’ve shared), we need a different approach.
Foundation Model Backbones
Fundamentally, all good ML architecture backbones have components for two important operations:
- Communication between tokens
- Computation within a token

The Transformer Block
In transformers, this is Attention (communication) and MLPs (computation). We improve transformers by optimising these two operations2.
We would like to replace the Attention component 3 with some other method for communicating between tokens. Mamba uses the Control Theory inspired SSM for Communication and keeps MLP-style projections for Computation.
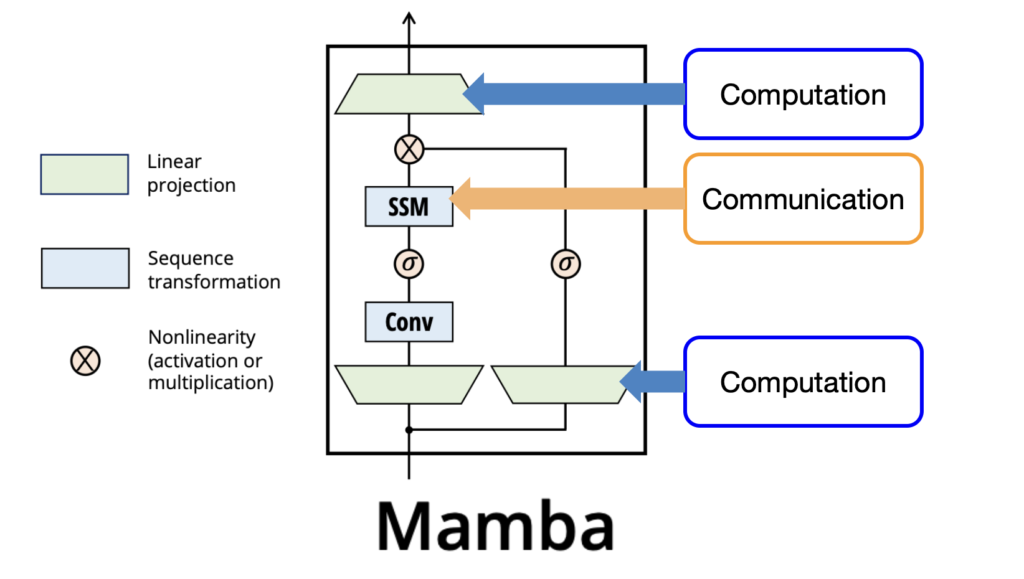
The Mamba Block
Like a Transformer made up of stacked transformer blocks, Mamba is made up of stacked Mamba blocks as above.
We would like to understand and motivate the choice of the SSM for sequence transformations.
Motivating Mamba – A Throwback to Temple Run
Imagine we’re building a Temple Run agent 4. It chooses if the runner should move left or right at any time.

To successfully pick the correct direction, we need information about our surroundings. Let’s call the collection of relevant information the state. Here the state likely includes your current position and velocity, the position of the nearest obstacle, weather conditions, etc.
Claim 1: if you know the current state of the world and how the world is evolving, then you can use this to determine the direction to move.
Note that you don’t need to look at the whole screen all the time. You can figure out what will happen to most of the screen by noting that as you run, the obstacles move down the screen. You only need to look at the top of the screen to understand the new information and then simulate the rest.
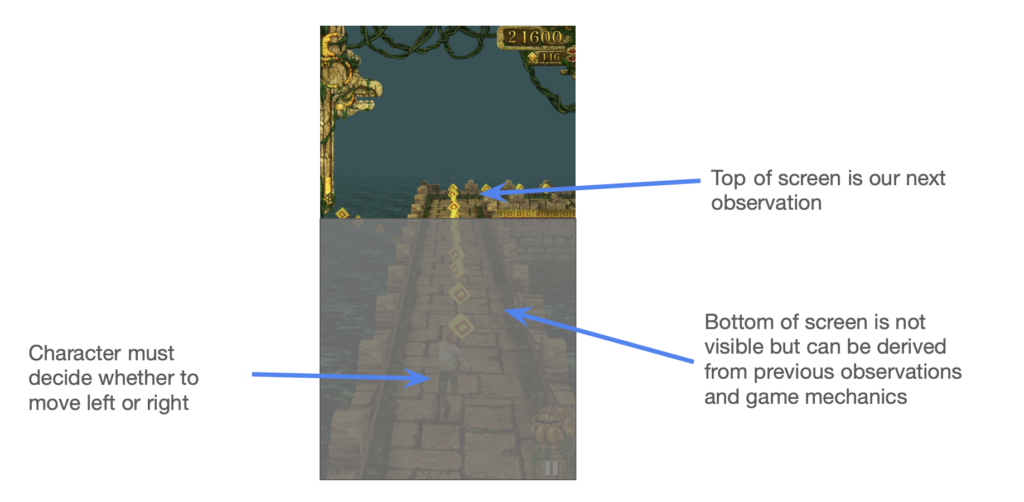
This lends itself to a natural formulation. Let h be the hidden state, relevant knowledge about the world. Also let x be the input, the observation that you get each time. h’ then represents the derivative of the hidden state, i.e. how the state is evolving. We’re trying to predict y, the optimal next move (right or left).
Now, Claim 1 states that from the hidden state h, h’, and the new observation x, you can figure out y.
More concretely, h, the state, can be represented as a differential equation (Eq 1a):
\[h’(t) = \mathbf{A}h(t) + \mathbf{B}x(t)\]
Knowing h allows you to determine your next move y (Eq 1b):
\[y(t) = \mathbf{C}h(t) + \mathbf{D}x(t)\]
The system evolves as a function of the current state and new observations. A small new observation is enough because we can determine most of the state by applying known state dynamics to the previous state. That is, most of the screen isn’t new, it’s just the natural downward movement of the previous state. Fully knowing the state would allow us to pick the best next move, y.
You can learn a lot about the system dynamics by observing the top of the screen – if it’s moving faster, we can infer the whole screen is and the game is speeding up5. In this way, even if we start off knowing nothing about the game except our limited observation, pretty soon we could understand the whole screen.
What’s the State?
Here, state refers to the variables that, when combined with the input variables, fully determine the future system behaviour. In theory, once we have the state, there’s nothing else we need to know about the past to predict the future. With this choice of state, the system is converted to a Markov Decision Process. Ideally, the state is a fairly small amount of information which captures the essential properties of the system. That is, the state is a compression of the past 6
Discretisation – How To Deal With Living in a Quantised World
Okay, great! So, given some state and input observation, we have an autoregressive-style system to determine the next action. Amazing!
In practice though, there’s a little snag here. We’re modelling time as continuous. But in real life, we get new inputs and take new actions at discrete time steps 7.

We would like to convert this continuous-time differential equation into a discrete-time difference equation. This conversion process is known as discretisation. Discretisation is a well-studied problem in the literature. Mamba uses the Zero-Order Hold (ZOH) discretisation8. To give an idea of what’s happening morally, consider a naive first-order approximation9.
From Equation 1a, we have
\[h’(t) = \mathbf{A}h(t) + \mathbf{B}x(t)\]
And for small ∆,
\[h’(t) \approx \frac{h(t+\Delta) – h(t)}{\Delta}\]
by the definition of the derivative.
We let:
\[h_t = h(t)\]
and
\[h_{t+1} = h(t + \Delta)\]
and substitute into Equation 1a giving:
\[h_{t+1} – h_t \approx \Delta (\mathbf{A}h_t + \mathbf{B}x_t)\] \[\Rightarrow h_{t+1} \approx (I + \Delta \mathbf{A})h_t + (\Delta \mathbf{B})x_t\]
Hence, after renaming the coefficients and relabelling indices, we have the discrete representations:
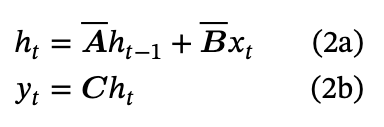
The Discretised Version of the SSM Equation
If you’ve ever looked at an RNN before 10 and this feels familiar – trust your instincts :
We have some input x, which is combined with the previous hidden state by some transform to give the new hidden state. Then we use the hidden state to calculate the output at each time step.
Understanding the SSM Matrices
Now, we can interpret the A, B, C, D matrices more intuitively:
- A is the transition state matrix. It shows how you transition the current state into the next state. It asks “How should I forget the less relevant parts of the state over time?”
- B is mapping the new input into the state, asking “What part of my new input should I remember?”. 11
- C is mapping the state to the output of the SSM. It asks, “How can I use the state to make a good next prediction?”. 12
- D is how the new input passes through to the output. It’s a kind of modified skip connection that asks “How can I use the new input in my prediction?”
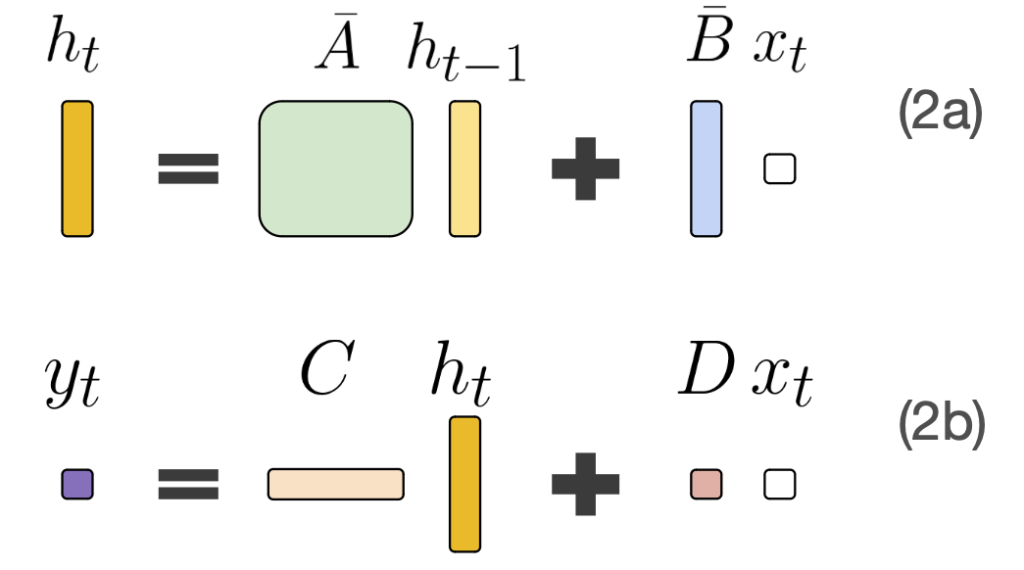
Visual Representation of The SSM Equations
Additionally, ∆ has a nice interpretation – it’s the step size, or what we might call the linger time or the dwell time. For large ∆, you focus more on that token; for small ∆, you skip past the token immediately and don’t include it much in the next state.

And that’s it! That’s the SSM, our ~drop-in replacement for Attention (Communication) in the Mamba block. The Computation in the Mamba architecture comes from regular linear projections, non-linearities, and local convolutions – the regular ML building blocks we know and love!
Okay great, that’s the theory – but does this work? Well…
Effectiveness vs Efficiency: Attention is Focus, Selectivity is Prioritisation
At WWDC ‘97, Steve Jobs famously noted that “focusing is about saying no”. Focus is ruthless prioritisation. It’s common to think about Attention positively as choosing what to notice. In the Steve Jobs sense, we might instead frame Attention negatively as choosing what to discard.
There’s a classic intuition pump in Machine Learning known as the Cocktail Party Problem 13. Imagine a party with dozens of simultaneous loud conversations:
Question:
How do we recognise what one person is saying when others are talking at the same time? 14
Answer:
The brain solves this problem by focusing your “attention” on a particular stimulus and hence drowning out all other sounds as much as possible.

Transformers use Dot-Product Attention to focus in on the most relevant tokens. A big reason Attention is so great is that you have the potential to look back at everything that ever happened in its context. This is like photographic memory when done right. 15
Transformers (🤖) are extremely effective. But they aren’t very efficient. They store everything from the past so that they can look back at tokens with theoretically perfect recall.
Traditional RNNs (🔁) are the opposite – they forget a lot, only recalling a small amount in their hidden state and discarding the rest. They are very efficient – their state is small. Yet they are less effective as discarded information cannot be recovered.
We’d like something closer to the Pareto frontier of the effectiveness/efficiency tradeoff. Something that’s more effective than traditional RNNs and more efficient than transformers.

The Mamba Architecture seems to offer a solution which pushes out the Pareto frontier of effectiveness/efficiency.
SSMs are as efficient as RNNs, but we might wonder how effective they are. After all, it seems like they would have a hard time discarding only unnecessary information and keeping everything relevant. If each token is being processed the same way, applying the same A and B matrices as if in a factory assembly line for tokens, there is no context-dependence. We would like the forgetting and remembering matrices (A and B respectively) to vary and dynamically adapt to inputs.
The Selection Mechanism
Selectivity allows each token to be transformed into the state in a way that is unique to its own needs. Selectivity is what takes us from vanilla SSM models (applying the same A (forgetting) and B (remembering) matrices to every input) to Mamba, the Selective State Space Model.
In regular SSMs, A, B, C and D are learned matrices – that is
\(\mathbf{A} = \mathbf{A}_{\theta}\) etc. (where θ represents the learned parameters)
With the Selection Mechanism in Mamba, A, B, C and D are also functions of x. That is \(\mathbf{A} = \mathbf{A}_{\theta(x)}\) etc; the matrices are context dependent rather than static.

Mamba (right) differs from traditional SSMs by allowing A,B,C matrices to be selective i.e. context dependent
Making A and B functions of x allows us to get the best of both worlds:
- We’re selective about what we include in the state, which improves effectiveness vs traditional SSMs.
- Yet, since the state size is bounded, we improve on efficiency relative to the Transformer. We have O(1), not O(n) space and O(n) not O(n²) time requirements.
The Mamba paper authors write:
The efficiency vs. effectiveness tradeoff of sequence models is characterized by how well they compress their state: efficient models must have a small state, while effective models must have a state that contains all necessary information from the context. In turn, we propose that a fundamental principle for building sequence models is selectivity: or the context-aware ability to focus on or filter out inputs into a sequential state. In particular, a selection mechanism controls how information propagates or interacts along the sequence dimension.
Humans (mostly) don’t have photographic memory for everything they experience within a lifetime – or even within a day! There’s just way too much information to retain it all. Subconsciously, we select what to remember by choosing to forget, throwing away most information as we encounter it. Transformers (🤖) decide what to focus on at recall time. Humans (🧑) also decide what to throw away at memory-making time. Humans filter out information early and often.
If we had infinite capacity for memorisation, it’s clear the transformer approach is better than the human approach – it truly is more effective. But it’s less efficient – transformers have to store so much information about the past that might not be relevant. Transformers (🤖) only decide what’s relevant at recall time. The innovation of Mamba (🐍) is allowing the model better ways of forgetting earlier – it’s focusing by choosing what to discard using Selectivity , throwing away less relevant information at memory-making time16.
The Problems of Selectivity
Applying the Selection Mechanism does have its gotchas though. Non-selective SSMs (i.e. A,B not dependent on x) are fast to compute in training. This is because the component of \(y_t\) which depends on \(x_i\) can be expressed as a linear map, i.e. a single matrix that can be precomputed!
For example (ignoring the D component, the skip connection):
\[y_2 = \mathbf{C}\mathbf{B}x_2 + \mathbf{C}\mathbf{A}\mathbf{B}x_1 + \mathbf{C}\mathbf{A}\mathbf{A}\mathbf{B}x_0\]
If we’re paying attention, we might spot something even better here – this expression can be written as a convolution. Hence we can apply the Fast Fourier Transform and the Convolution Theorem to compute this very efficiently on hardware as in Equation 3 below.
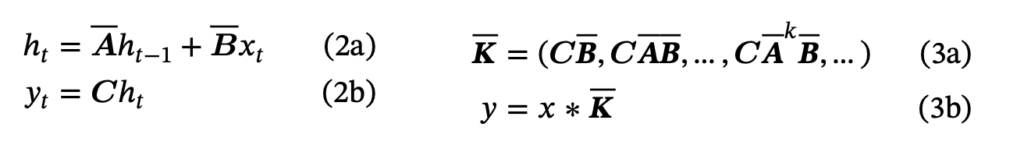
We can calculate Equation 2, the SSM equations, efficiently in the Convolutional Form, Equation 3.
Unfortunately, with the Selection Mechanism, we lose the convolutional form. Much attention is given to making Mamba efficient on modern GPU hardware using similar hardware optimisation tricks to Tri Dao’s Flash Attention 17. With the hardware optimisations, Mamba is able to run faster than comparably sized Transformers.
Machine Learning for Political Economists – How Large Should The State Be?
The Mamba authors write, “the efficiency vs. effectiveness tradeoff of sequence models is characterised by how well they compress their state”. In other words, like in political economy18, the fundamental problem is how to manage the state.
🔁 Traditional RNNs are anarchic
They have a small, minimal state. The size of the state is bounded. The compression of state is poor.
🤖 Transformers are communist
They have a maximally large state. The “state” is just a cache of the entire history with no compression. Every context token is treated equally until recall time.
🐍 Mamba has a compressed state
…but it’s selective about what goes in. Mamba says we can get away with a small state if the state is well focused and effective 19.
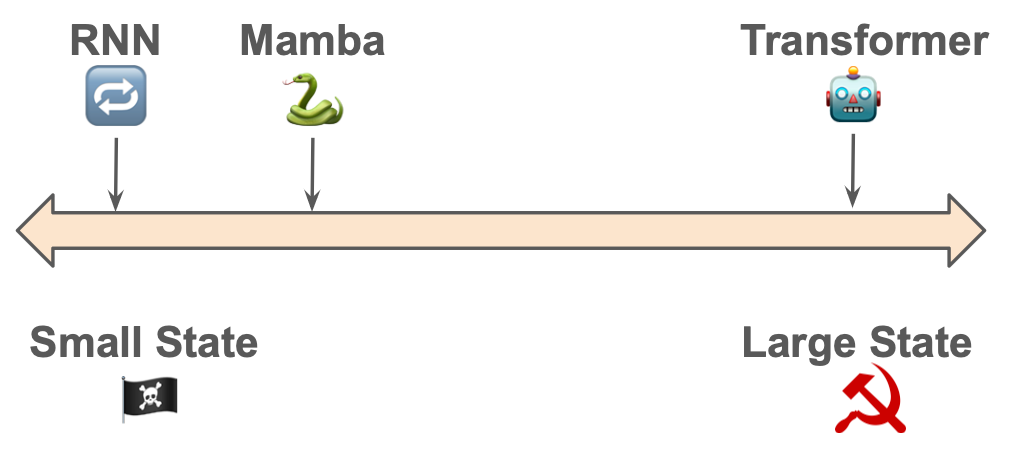
Language Models and State Size
The upshot is state representation is critical. A smaller state is more efficient; a larger state is more effective. The key is to selectively and dynamically compress data into the state. Mamba’s Selection Mechanism allows for context-dependent reasoning, focusing and ignoring. For both performance and interpretability, understanding the state seems to be very useful.
Information Flow in Transformer vs Mamba
How do Transformers know anything? At initialisation, a transformer isn’t very smart. It learns in two ways:
- Training data (Pretraining, SFT, RLHF etc)
- In context-data
Training Data
Models learn from their training data. This is a kind of lossy compression of input data into the weights. We can think of the effect of pretraining data on the transformer kinda like the effect of your ancestor’s experiences on your genetics – you can’t recall their experiences, you just have vague instincts about them 20.
In Context-Data
Transformers use their context as short-term memory, which they can recall with ~perfect fidelity. So we get In-Context Learning, e.g. using induction heads to solve the Indirect Object Identification task, or computing Linear Regression.
Retrieval
Note that Transformers don’t filter their context at all until recall time. So if we have a bunch of information we think might be useful to the Transformer, we filter it outside the Transformer (using Information Retrieval strategies) and then stuff the results into the prompt. This process is known as Retrieval Augmented Generation (RAG). RAG determines relevant information for the context window of a transformer. A human with the internet is kinda like a RAG system – you still have to know what to search but whatever you retrieve is as salient as short-term memory to you.
Information Flow for Mamba
Training Data acts similarly for Mamba. However, the lines are slightly blurred for in-context data and retrieval. In-context data for Mamba is compressed/filtered similar to retrieval data for transformers. This in-context data is also accessible for look-up like for transformers (although with somewhat lower fidelity).

Transformer context is to Mamba states what short-term is to long-term memory. Mamba doesn’t just have “RAM”, it has a hard drive21 22.
Swapping States as a New Prompting Paradigm
Currently, we often use RAG to give a transformer contextual information.
With Mamba-like models, you could instead imagine having a library of states created by running the model over specialised data. States could be shared kinda like LoRAs for image models.
For example, I could do inference on 20 physics textbooks and, say, 100 physics questions and answers. Then I have a state which I can give to you. Now you don’t need to add any few-shot examples; you just simply ask your question. The in-context learning is in the state.
In other words, you can drag and drop downloaded states into your model, like literal plug-in cartridges. And note that “training” a state doesn’t require any backprop. It’s more like a highly specialised one-pass fixed-size compression algorithm. This is unlimited in-context learning applied at inference time for zero-compute or latency. 23
The structure of an effective LLM call goes from…
- System Prompt
- Preamble
- Few shot-examples
- Question
…for Transformers, to simply…
- Inputted state (with problem context, initial instructions, textbooks, and few-shot examples)
- Short question
…for Mamba.
This is cheaper and faster than few-shot prompting (as the state is infinitely reusable without inference cost). It’s also MUCH cheaper than finetuning and doesn’t require any gradient updates. We could imagine retrieving states in addition to context.
Mamba & Mechanistic Interpretability
Transformer interpretability typically involves:
- understanding token relationships via attention,
- understanding circuits, and
- using Dictionary Learning for unfolding MLPs.
Most of the ablations that we would like to do for Mamba are still valid, but understanding token communication (1) is now more nuanced. All information moves between tokens via hidden states instead of the Attention Mechanism which can “teleport” information from one sequence position to another.
For understanding in-context learning (ICL) tasks with Mamba, we will look to intervene on the SSM state. A classic task in-context learning task is Indirect Object Identification in which a model has to finish a paragraph like:
Then, Shelby and Emma had a lot of fun at the school. [Shelby/Emma] gave an apple to [BLANK]
The model is expected to fill in the blank with the name that is not repeated in the paragraph. In the chart below we can see that information is passed from the [Shelby/Emma] position to the final position via the hidden state (see the two blue lines in the top chart).
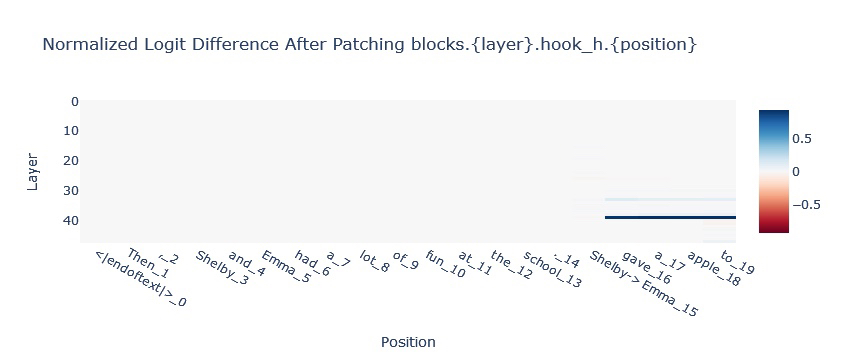
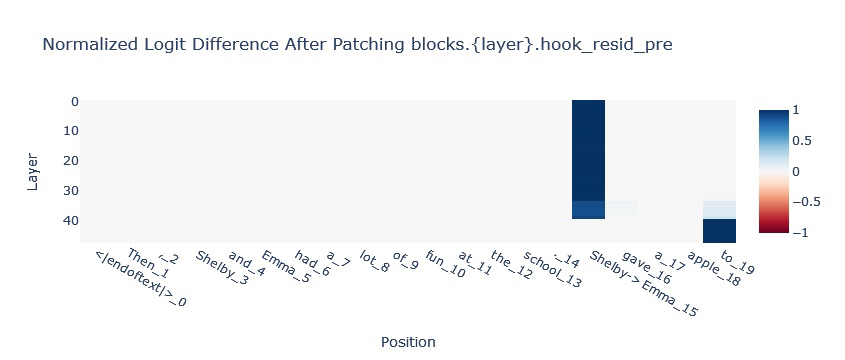
Since it’s hypothesised that much of In-Context Learning in Transformers is downstream of more primitive sequence position operations (like Induction Heads), Mamba being able to complete this task suggests a more general In-Context Learning ability.
What’s Next for Mamba & SSMs?
Mamba-like models are likely to excel in scenarios requiring extremely long context and long-term memory. Examples include:
- Processing DNA
- Generating (or reasoning over) video
- Writing novels
An illustrative example is agents with long-term goals.
Suppose you have an agent interacting with the world. Eventually, its experiences become too much for the context window of a transformer. The agent then has to compress or summarise its experiences into some more compact representation.
But how do you decide what information is the most useful as a summary? If the task is language, LLMs are actually fairly good at summaries – okay, yeah, you’ll lose some information, but the most important stuff can be retained.
However, for other disciplines, it might not be clear how to summarise. For example, what’s the best way to summarise a 2 hour movie? 24. Could the model itself learn to do this naturally rather than a hacky workaround like trying to describe the aesthetics of the movie in text?
This is what Mamba allows. Actual long-term memory. A real state where the model learns to keep what’s important. Prediction is compression – learning what’s useful to predict what’s coming next inevitably leads to building a useful compression of the previous tokens.
The implications for Assistants are clear:
Your chatbot co-evolves with you. It remembers.
Agents & AI Safety
One reason for positive updates in existential risk from AGI is Language Models. Previously, Deep-RL agents trained via self-play looked set to be the first AGIs. Language models are inherently much safer since they aren’t trained with long-term goals. 25
The potential for long-term sequence reasoning here brings back the importance of agent-based AI safety. Few agent worries are relevant to Transformers with an 8k context window. Many are relevant to systems with impressive long-term memories and possible instrumental goals.
The Best Collab Since Taco Bell & KFC: 🤖 x 🐍
The Mamba authors show that there’s value in combining Mamba’s long context with the Transformer’s high fidelity over short sequences. For example, if you’re making long videos, you likely can’t fit a whole movie into a Transformer’s context for attention 26. You could imagine having Attention look at the most recent frames for short-term fluidity and an SSM for long-term narrative consistency 27.
This isn’t the end for Transformers. Their high effectiveness is exactly what’s needed for many tasks. But now Transformers aren’t the only option. Other architectures are genuinely feasible.
So we’re not in the post-Transformer era. But for the first time, we’re living in the post-only-Transformers era 28. And this blows the possibilities wide open for sequence modelling with extreme context lengths and native long-term memory.
All that remains to ask is: Is Attention All We Need?
Thanks to Gonçalo for reading an early draft, Jaden for the nnsight library used for the Interpretability analysis and Tessa for Mamba patching visualisations.
Also see:Mamba paper, Mamba Python code, Annotated S4, Nathan Labenz podcast
