F1 score is a measure of the harmonic mean of precision and recall. Commonly used as an evaluation metric in binary and multi-class classification, the F1 score integrates precision and recall into a single metric to gain a better understanding of model performance.

F-score can be modified into F0.5, F1, and F2 based on the measure of weightage given to precision over recall depending on your use case.

Why Is F1 Score Useful?

There are a number of metrics useful for measuring performance of classification models. Accuracy is one of the simplest to understand. The accuracy metric measures the number of times a model was able to correctly identify the data class across the entire dataset. Accuracy is a reliable metric as long as your dataset has an equal number of samples for each class.

Nevertheless, this scenario is hard to imagine with the real world datasets. Imagine you have a dataset where 99% of the records belong to Class A and the rest (1%) to Class B – a common occurrence in areas like credit card fraud where almost all transactions are non-fraudulent. Regardless of the sample from this type of dataset, the accuracy will still be 99%. Leveraging accuracy is not ideal in this scenario.

For imbalanced data, F1 score comes to rescue. It takes into account the type of errors — false positive and false negative – and not just the number of predictions that were incorrect.

How Do Precision and Recall Relate to F1 Score?

F1 score computes the average of precision and recall, where the relative contribution of both of these metrics are equal to F1 score. The best value of F1 score is 1 and the worst is 0. What does this mean? This means a perfect model will have a F1 score of 1 – all of the predictions were correct.

As precision and recall both are rates, F1 score uses harmonic mean rather than a common arithmetic average. Let’s see how it uses both of these metrics and why.

Precision

Precision is a model performance metric that corresponds to the fraction of values that actually belong to a positive class out of all of the values which are predicted to belong to that class. Precision is also known as the positive predictive value (PPV).

F1 score uses precision to get the rate of true positive records among the total records classified as positive by machine learning model. Precision is calculated as below:

Machine learning models may find a lot of the positives, but it can wrongly detect positives that aren’t actually positives. Sometimes, they can fail to find all the positives, and the ones identified as positive are likely to be correct.

Recall

Recall is a performance metric that corresponds to the fraction of values predicted to be of a positive class out of all the values that truly belong to the positive class (including false negatives).

F1 score uses recall to get the fraction of true positive records among the total of actual positive records. Recall is calculated as below:

A machine learning model with high recall means that there are positive cases in the data, though there can be negative cases identified as positive cases. Low recall indicates that it was not able to find any positive case.

How Is the F1 Score Calculated Using Precision and Recall?

F1 score combines both of these precision and recall and symmetrically represents them in the formula:

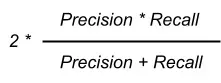
As mentioned above F1 scores can range from 0 to 1, with 1 representing a model that perfectly classifies each observation into the correct class and 0 representing a model that is unable to classify any observation into the correct class.

Suppose you have a machine learning model to predict if a credit card transaction was fraudulent or not. The following confusion matrix summarizes the prediction made by the model:

Total No. of Records165 Actual Positives Actual Negatives
Predicted Positives True Positives 50 False Positives 10
Predicted Negatives False Negatives 5 True Negatives 100

You can calculate Precision and Recall as below:

Precision = 50 / 50+10 = 0.83

Recall = 50 / 50+5 = 0.91

Let’s put these together in F1 score formula:

F1 Score = 2 * (0.83 * 0.91) / 0.83 + 0.91 = 0.87

Our model has an F1 Score of 0.87, which is close to 1 (which means all predictions are correct). Using the harmonic mean in F1 Score, we find a balance of similar values for precision and recall. The more the precision and recall scores deviate from each other, the worse the F1 score will be.

In Which Real-World Applications is F1 Score Most Useful?

F1 score is a common metric to use in binary and multiclass classification problems as it balances precision and recall. Below are a few examples of where it can be useful.

Healthcare

In healthcare, F1 score can sometimes be useful for models that aim to suggest a diagnosis (i.e. from scanning electronic medical records). A high F1 score indicates that the model is good at identifying both positive and negative cases, which can be important for minimizing misdiagnosis and ensuring patients receive proper treatment.

Fraud Detection

As a general rule, fraud accounts for a relatively small portion of transactions in the real world. In healthcare billing, for example, fraud is estimated to be 3% of total transactions. As a result, traditional accuracy metrics can be misleading. F1 score can be useful in such cases. However, practitioners may want to adjust the weight of the F score. In credit card fraud, for example, a misclassified fraudulent transaction (a false negative — predicting “not fraud” for a transaction that is indeed fraud) is often more costly given its direct impacts on revenue than a misclassified legitimate transaction (a false positive — predicting fraud for a transaction that is not fraud), where a customer is merely inconvenienced.

Spam Classification

In email spam classification, it is important to both correctly identify spam emails while minimizing false positives (emails falsely flagged as spam). F1 score is often preferred over other metrics – such as accuracy, precision, or recall – for spam classification for that reason and because it is an imbalanced classification problem where the number of spam emails is much smaller than the number of non-spam emails.

When Should F1 Score Be Avoided in Favor of Other Metrics?

It’s important to note F1 score’s limitations. While the F1 score offers a way to compare classifiers with a single metric, in the process important differences can get obscured since it assigns an equal weight to both precision and recall. In some domains, such as identifying faulty components for a crane or corrosion on a bridge, there cannot be false negatives. In these scenarios, it would make sense to have a model incorrectly flag dozens of perfectly safe components rather than risk letting even one unsafe component through the process. In such a scenario, recall might be more useful since it minimizes false negatives.

Hands-On Exercise: Create a Classifier and Measure Its Performance with F1 Score

In the previous sections, we got familiar with F1 Score and learned how it can be used as a performance metric for a model when we have imbalanced data. In this section, we will go through steps of creating a classifier and how to measure its performance using F1 score and make the correct decision.

Create A Classification Model

STEP ONE : load the data

    # Load the data from Kaggle

    !pip install kaggle

    from google.colab import files
    files.upload() #Upload Kaggle.json file

    !mkdir -p ~/.kaggle
    !cp kaggle.json ~/.kaggle/

    !kaggle datasets download -d mlg-ulb/creditcardfraud
    !unzip creditcardfraud.zip

    import pandas as pd
    df = pd.read_csv("creditcard.csv")
    print(df.columns)
    print(df.head(5))

STEP TWO : Confirm the “Class” distribution

# Check class distribution in the data
class_names = {0:'Not Fraud', 1:'Fraud'}
print(df.Class.value_counts().rename(index = class_names))

As you can see, we only have 492 records classified as “Fraudulent.” Notice how imbalanced the dataset is. If we use this dataset, our model might end up overfitting and classify most of the data as “Not Fraud.”

STEP THREE : Most of the data is scaled, except Time and Amount. Let’s scale these:

from sklearn.preprocessing import StandardScaler, RobustScaler
    
std_scaler = StandardScaler()
rob_scaler = RobustScaler()
    
df['scaled_amount'] = rob_scaler.fit_transform(df['Amount'].values.reshape(-1,1))
df['scaled_time'] = rob_scaler.fit_transform(df['Time'].values.reshape(-1,1))
    
df.drop(['Time','Amount'], axis=1, inplace=True)
    
scaled_amount = df['scaled_amount']
scaled_time = df['scaled_time']
    
df.drop(['scaled_amount', 'scaled_time'], axis=1, inplace=True)
df.insert(0, 'scaled_amount', scaled_amount)
df.insert(1, 'scaled_time', scaled_time)

STEP FOUR : Next, let’s split the data into training, validation and testing datasets to be able to train the model on different sub-samples of the dataset.

from sklearn.model_selection import train_test_split

X = df.drop('Class', axis=1)
y = df['Class']

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, random_state=42)


print("Length of X_train is: {X_train}".format(X_train = len(X_train)))
print("Length of X_test is: {X_test}".format(X_test = len(X_test)))
print("Length of X_val is: {X_val}".format(X_val = len(X_val)))

print("Length of y_train is: {y_train}".format(y_train = len(y_train)))
print("Length of y_test is: {y_test}".format(y_test = len(y_test)))
print("Length of y_val is: {y_val}".format(y_val = len(y_val)))

STEP FIVE : Create a classification model

    from sklearn.linear_model import LogisticRegression
    
    model = LogisticRegression(max_iter=3000, verbose=False).fit(X_train, y_train)

STEP SIX : Now, let’s make some predictions and see how our model performed

    #Use the model to generate predictions
    y_train_pred = model.predict(X_train)
    y_val_pred = model.predict(X_val)
    y_test_pred = model.predict(X_test)
    
    from sklearn.metrics import f1_score, recall_score, accuracy_score
    
    f1_score = round(f1_score(y_test, y_test_pred), 2)
    recall_score = round(recall_score(y_test, y_test_pred), 2)
    accuracy_score = accuracy_score(y_true, y_pred)
    
    print("Sensitivity/Recall for Logistic Regression Model 1 : {recall_score}".format(recall_score = recall_score))
    
    print("F1 Score for Logistic Regression Model 1 : {f1_score}".format(f1_score = f1_score))
    
    print("Accuracy Score for Logistic Regression Model 1 : {accuracy_score}".format(accuracy_score = accuracy_score))

If you look at the accuracy score, as suspected the model is overfitting the data and showing 99% accuracy because of the data imbalance. But look at the F1-score, showing the actual performance of the model. This could be the benchmark for us, when we continue to run the model with a new set of data and retrain it.

Summary

In the real world, we hardly get balanced data and most of the time we have to train our models using imbalanced data. There are ways to deal with imbalanced data (e.g. SMOTE), but how can you make sure that those techniques are also working? In practice, we often need F1-score as it takes recall and precision both into account.

In this article we got familiarized with F1-score, how it is calculated and applications where it is useful or not. We also saw how to create a model, predict the values and find the performance of that model using different performance metrics and monitor it.