 Image by author using DALL-E 3.
Image by author using DALL-E 3.
The advent of transformers in 2017 set off a landslide of AI milestones, starting with the spectacular achievements of large language models (LLMs) in natural language processing (NLP), and quickly catalyzing advancement in other domains such as computer vision and robotics. The unification of NLP and computer vision problems into a common architecture accelerated efforts in learning joint vision-language representation spaces, which enabled the seminal achievements in vision-language modeling surrounding contrastive language-image pretraining (CLIP) in 2021, and lead to the birth of large multimodal models (LMMs).
This dawning era of large models has demonstrated awe-inspiring capabilities and marked several major strides toward artificial general intelligence (AGI), but the enormous size of these models makes them difficult to deploy. As with many transformative technologies before them, the alluring capabilities of LLMs were at first accessible only to those with the resources to operate at the bleeding edge of technology. While private research has continued to push the limits of performance using LMMs with hundreds of billions of parameters, open-source research has established a pattern of catching up to these watermarks using much smaller models.
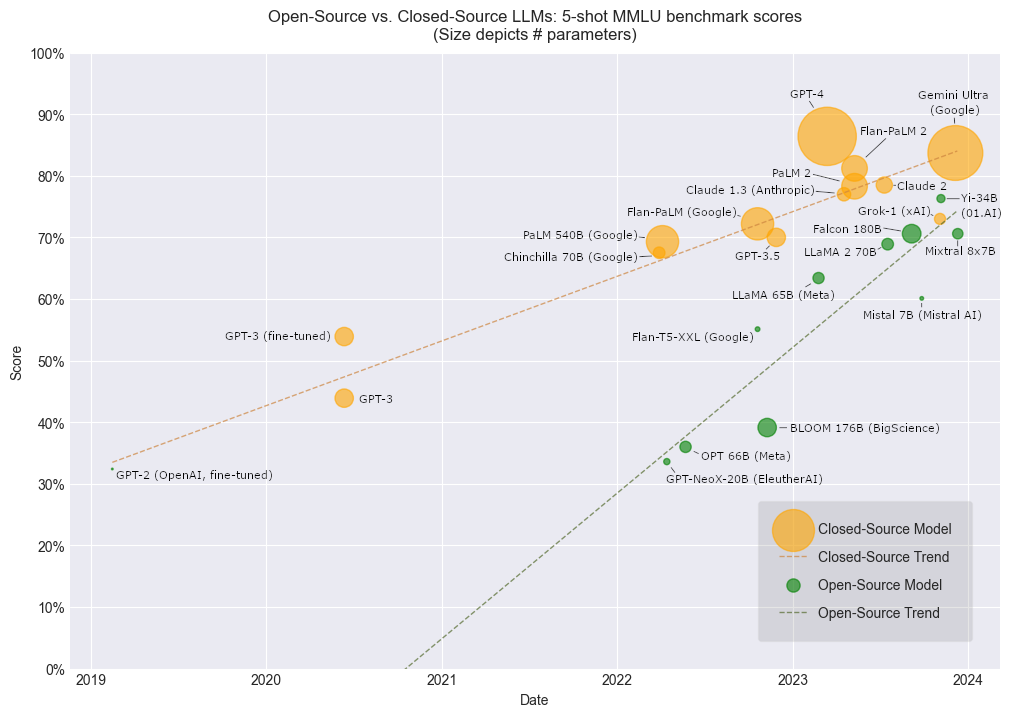
Image by author. Over time, open-source LLMs are closing the performance gap with much smaller sizes.
Even with this increasing potency, however, the smallest LLMs will not fit on consumer GPUs for inference, let alone be trained, without model compression techniques being applied. Fortunately, the tantalizing capabilities of these models have driven researchers to find effective methods for squeezing them into smaller spaces. Thanks to their efforts, we can now deploy LLMs easily on consumer hardware, as well as fine-tune them to our desired use cases, without requiring the resources of the corporate titans. This series provides a comprehensive review of four model compression techniques that enable LLM inference and fine-tuning in resource-constrained environments, outlined below:
Model Compression Techniques for LLMs
- Pruning — removal of network parameters individually (unstructured) or in groups (structured) based on their importance in order to decrease model complexity while maintaining accuracy.
- Quantization — discretizing and/or reducing the resolution of the numeric space of the weights to save space and ease computation.
- Knowledge Distillation — small models trained to target the learned functions of large experts can be trained with unlabeled data and outperform similar small models trained on the original task.
- Parameter-Efficient Fine-Tuning — reduces the number of trainable parameters required to fine-tune a model for task-specific behavior.
Each of these techniques has been shown to greatly increase efficiency of large models with relatively innocuous effects on performance, bringing the awe-inspiring powers of the large pre-trained language model (PLM) colossus down to earth where they can be used by anyone. Here we explore each technique in detail, so that we are empowered to employ them in our own work. Like LLMs, these topics can only be compressed to a certain extent before significant loss of knowledge occurs. Hence, we will break this discussion into a series of articles to give each of these techniques the space it deserves, and properly review these rich legacies of research which together provide us with powerful channels for bringing fire to mankind.
In this article, we start at the beginning with the oldest technique on our list, almost as old as the backpropagation-trained neural networks that it compresses: pruning. First, a quick journey through the history of pruning will teach us the distinctions between unstructured and structured pruning techniques, along with their comparative strengths and weaknesses. Equipped with this prerequisite knowledge, we then review the application of these approaches in today’s world of LLMs, and offer closing thoughts.
The forthcoming installments in the Streamlining Giants series will provide similar dives into each of the remaining compression techniques: quantization, knowledge distillation, and parameter-efficient fine-tuning, elucidating a clear and comprehensive understanding of each so that we can approach the game of LLM development playing with a full deck.
Pruning

Image by author using DALL-E 3.
The quest to refine neural networks for practical applications traces its roots back to the foundational days of the field. When Rumelhart, Hinton, and Williams first demonstrated how to use the backpropagation algorithm to successfully train multi-layer neural networks that could learn complex, non-linear representations in 1986, the vast potential of these models became apparent. However, the computational power available in the 1980s restricted their practical use and the complexity of problems they could solve, a situation which mirrors the challenges we face with deploying LLMs today. Although the scale of models and the considerations being made were very different, early discoveries in network minimization would pave the way for big wins in model compression decades later. In this section, we take a brief journey through the history and motivations driving pruning research, discover the comparative strengths and weaknesses of unstructured versus structured methods, and prepare ourselves to explore their use in the modern era of LLMs.
Network pruning was originally motivated by the pursuit of better model generalization through freezing unimportant weights at zero, somewhat akin in theory to L1/Lasso and L2/Ridge regularization in linear regression, though different in that weights are selected and hard-set to zero (pruned) after training based on an importance criteria rather than being coaxed towards zero mathematically by the loss function during training (informed readers will know that regularization can also be achieved in neural network training using weight decay ).
The common motivation behind both regularization and pruning (which can be seen as a form of regularization) is the theoretical and empirical evidence that neural networks are most effective at learning when overparameterized thanks to a higher-dimensional manifold of the loss function’s global minima and a larger exploration space in which effective subnetworks are more likely to be initialized (see “the lottery ticket hypothesis”). However, this overparameterization in turn leads to overfitting on the training data, and ultimately results in a network with many redundant or inactive weights. Although the theoretical mechanisms underlying the “unreasonable effectiveness” of overparameterized neural networks were less well studied at the time, researchers in the 1980s correctly hypothesized that it should be possible to remove a large portion of the network weights after training without significantly affecting task performance, and that performing iterative rounds of pruning and fine-tuning the remaining model weights should lead to better generalization, enhancing the model’s ability to perform well on unseen data.
Unstructured Pruning
To select parameters for removal, a measure of their impact on the cost function, or “saliency,” is required. While the earliest works in network minimization worked under the assumption that the magnitude of parameters should serve as a suitable measure of their saliency, LeCun et al. made a significant step forward in 1989 with “Optimal Brain Damage” (OBD), in which they proposed to use a theoretically justifiable measure of saliency using second-derivative information of the cost function with respect to the parameters, allowing them to directly identify the parameters which could be removed with the least increase in error.
Written in the era when the model of interest was a fully-connected neural network containing just 2,600 parameters, the authors of OBD were less concerned about removing weights due to computational efficiency than we are today with our billionaire behemoths, and were more interested in improving the model’s ability to generalize to unseen data by reducing model complexity. Even operating on a tiny model like this, however, the calculation of second-derivative information (Hessian matrix) is very expensive, and required the authors to make three convenient mathematical assumptions: 1) that the model is currently trained to an optimum, meaning the gradient of the loss with respect to every weight is currently zero and the slope of the gradient is positive in both directions, which zeroes out the first-order term of the Taylor expansion and implies the change in loss caused by pruning any parameter is positive, 2) that the Hessian matrix is diagonal, meaning the change in loss caused by removal of each parameter is independent, and therefore the loss deltas can be summed over subset of weights to calculate the total change in loss caused by their collective removal, and 3) that the loss function is nearly quadratic, meaning higher-order terms can be neglected from the Taylor expansion.
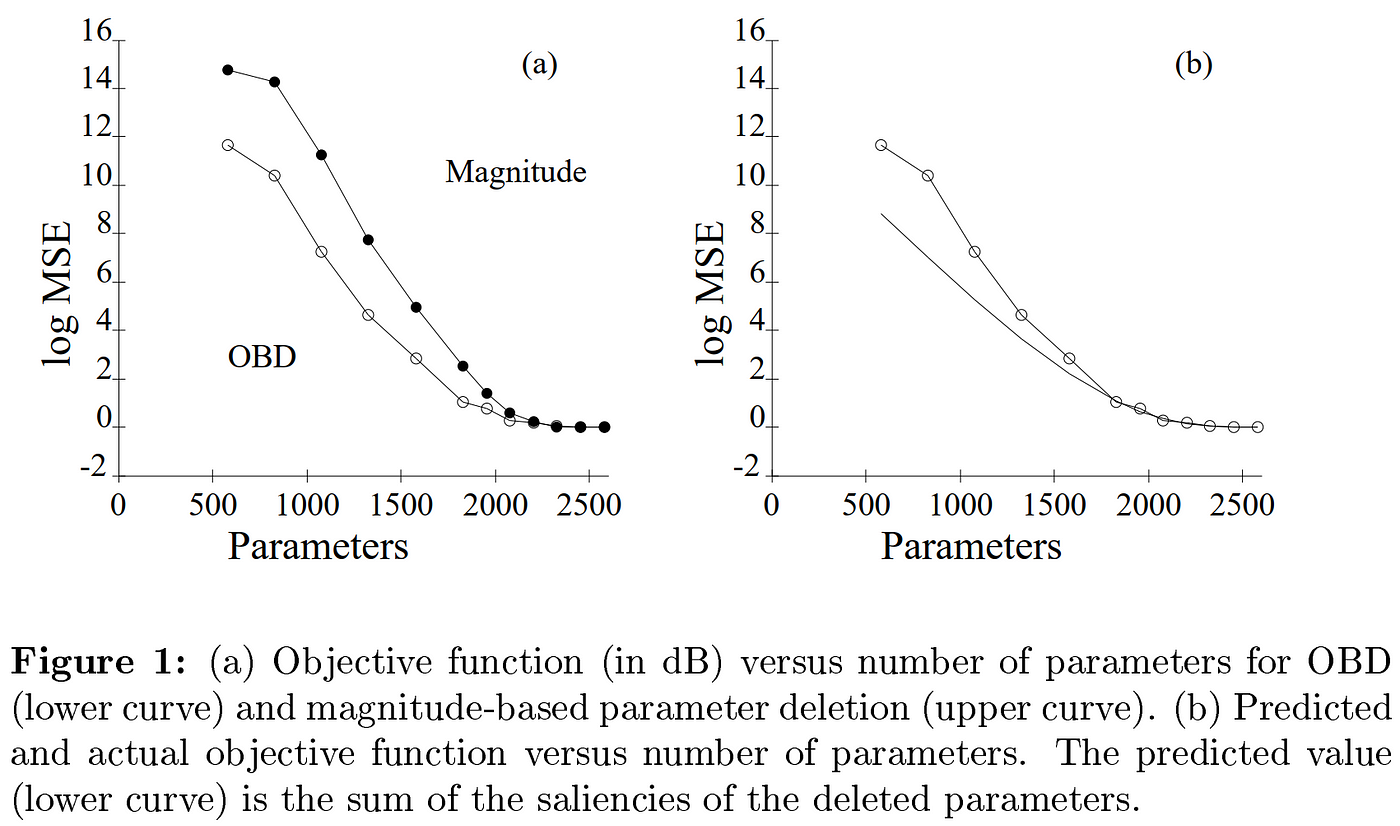
Results from OBD are superior to magnitude-based pruning (left). Accuracy of OBD saliency estimation (right).
Despite this requisite list of naïve assumptions, their theoretically justified closed-form saliency metric proved itself superior to magnitude-based pruning in accurately identifying the least important weights in a network, able to retain more accuracy at higher rates of compression. Nevertheless, the efficacy and profound simplicity of magnitude-based pruning methods would make them the top choice for many future research endeavors in model compression, particularly as network sizes began to scale quickly, and Hessians became exponentially more frightening. Still, this successful demonstration of using a theoretically justified saliency measure to more accurately estimate saliency and thereby enable more aggressive pruning provided an inspirational recipe for future victories in model compression, although it would be some time before those seeds bore fruit.
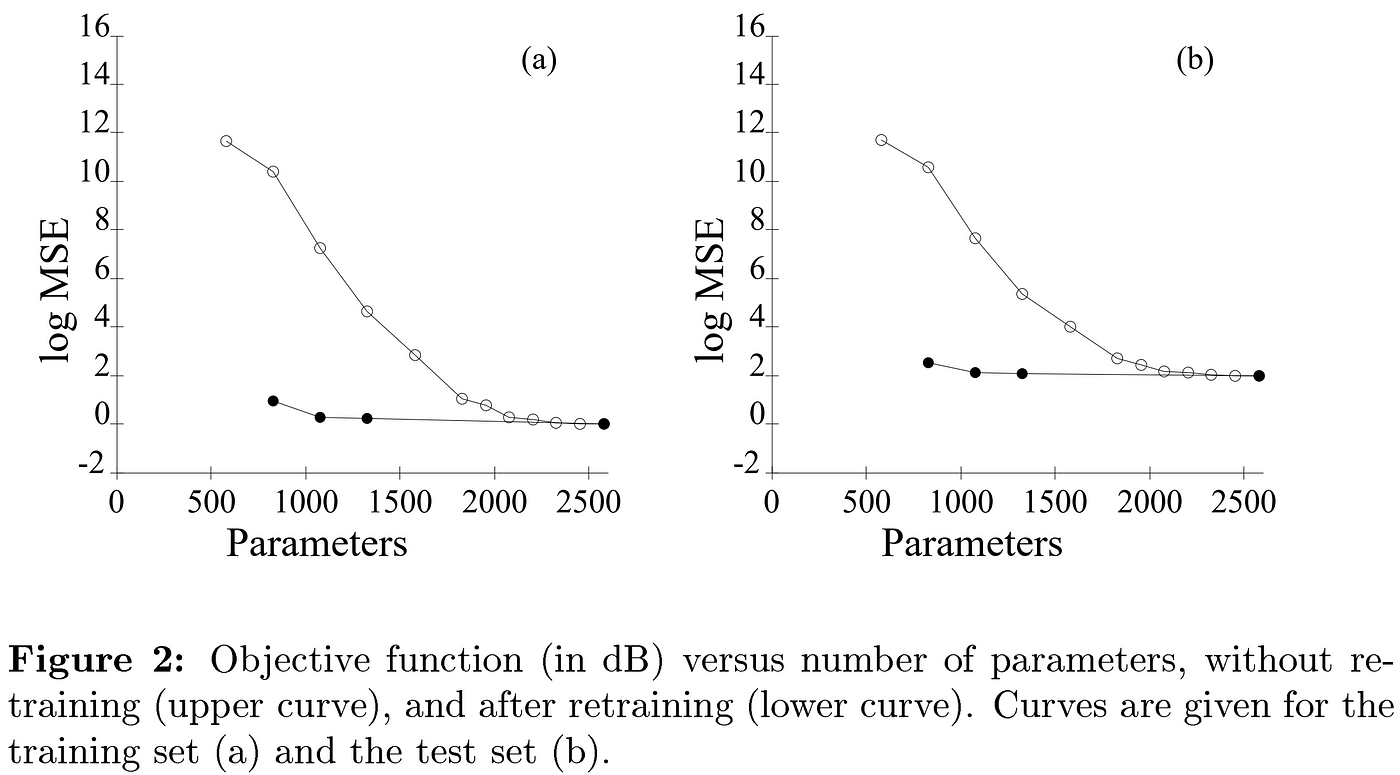
Results from OBD show that repeated iterations of pruning and fine-tuning preserve original performance levels even down to less than half the original parameter count. The implications in the context of today’s world of large models is clear, but they were more interested in boosting model generalization.
Four years later in 1993, Hassibi et al.’s Optimal Brain Surgeon (OBS) expanded on the concept of OBD and raised the levels of compression possible without increasing error by eschewing the diagonality assumption of OBD and instead considering the cross-terms within the Hessian matrix. This allowed them to determine optimal updates to the remaining weights based on the removal of a given parameter, simultaneously pruning and optimizing the model, thereby avoiding the need for a retraining phase. However, this meant even more complex mathematics, and OBS was thus initially of limited utility to 21st Century researchers working with much larger networks. Nonetheless, like OBD, OBS would eventually see its legacy revived in future milestones, as we will see later.
The pruning methods in OBD and OBS are examples of unstructured pruning , wherein weights are pruned on an individual basis based on a measure of their saliency. A modern exemplar of unstructured pruning techniques is Han et al. 2015, which reduced the sizes of the early workhorse convolutional neural networks (CNNs) AlexNet and VGG-16 by 9x and 13x, respectively, with no loss in accuracy, using one or more rounds of magnitude-based weight pruning and fine-tuning. Their method unfortunately requires performing sensitivity analysis of the network layers to determine the best pruning rate to use for each individual layer, and works best when retrained at least once, which means it would not scale well to extremely large networks. Nevertheless, it is impressive to see the levels of pruning which can be accomplished using their unstructured approach, especially since they are using magnitude-based pruning. As with any unstructured approach, the reduced memory footprint can only be realized by using sparse matrix storage techniques which avoid storing the zeroed parameters in dense matrices. Although they do not employ it in their study, the authors mention in their related work section that the hashing trick (as demonstrated in the 2015 HashedNets paper) is complementary to unstructured pruning, as increasing sparsity decreases the number of unique weights in the network, thereby reducing the probability of hash collisions, which leads to lower storage demands and more efficient weight retrieval by the hashing function.
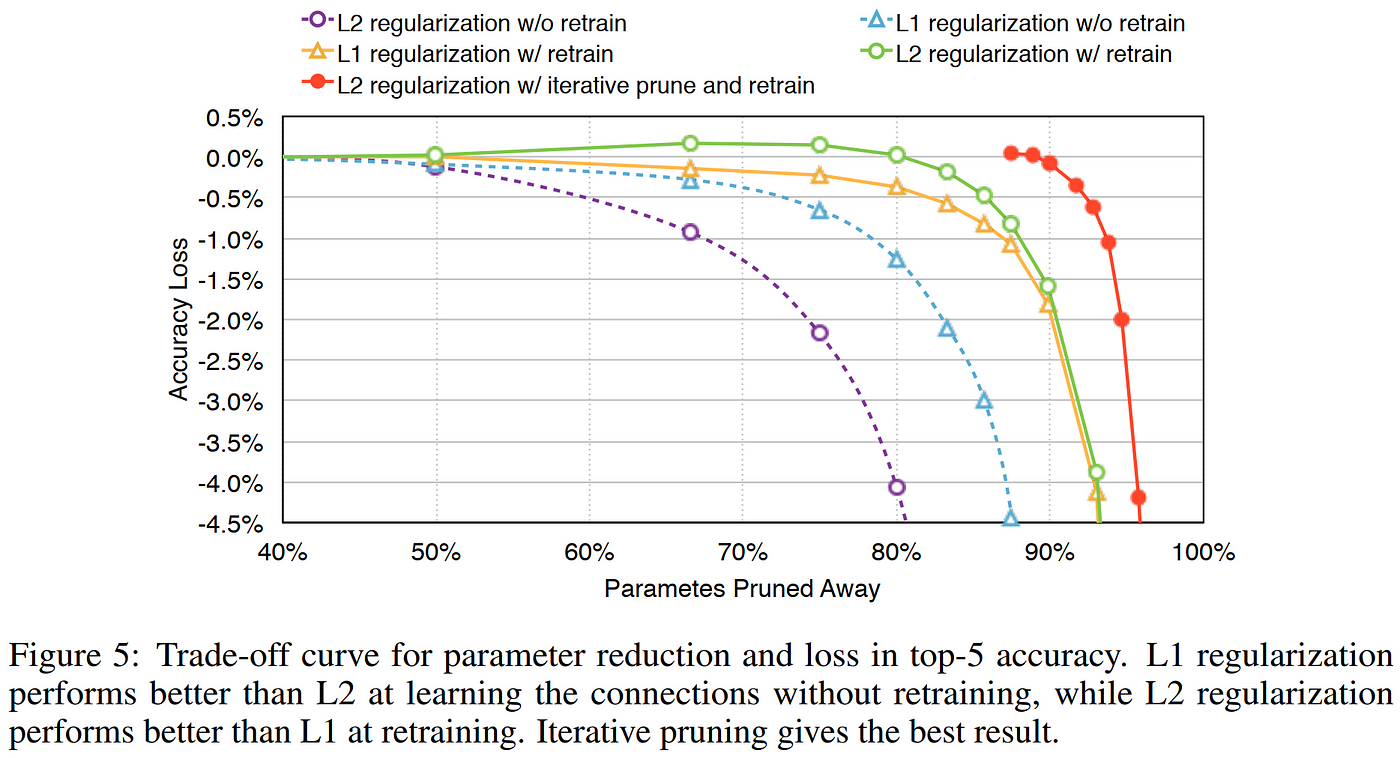
Results from Han et al. 2015 show the power of unstructured pruning in CNNs of the time period. Notice the “free lunch” compression of 40–50% of parameters pruned away with no accuracy loss and no retraining.
While unstructured pruning has the intended regularization effect of improved generalization through reduced model complexity, and the memory footprint can then be shrunk substantially by using sparse matrix storage methods, the gains in computational efficiency offered by this type of pruning are not so readily accessed. Simply zeroing out individual weights without consideration of the network architecture will create matrices with irregular sparsity that will realize no efficiency gains when computed using dense matrix calculations on standard hardware. Only specialized hardware which is explicitly designed to exploit sparsity in matrix operations can unlock the computational efficiency gains offered by unstructured pruning. Fortunately, consumer hardware with these capabilities is becoming more mainstream, enabling their users to actualize performance gains from the sparse matrices created from unstructured pruning. However, even these specialized hardware units must impose a sparsity ratio expectation on the number of weights in each matrix row which should be pruned in order to allow for the algorithmic exploitation of the resulting sparsity, known as semi-structured pruning , and enforcing this constraint has been shown to degrade performance more than purely unstructured pruning.
Structured Pruning
We’ve seen that unstructured pruning is a well-established regularization technique that is known to improve model generalization, reduce memory requirements, and offer efficiency gains on specialized hardware. However, the more tangible benefits to computational efficiency are offered by structured pruning , which entails removing entire structural components (filters, layers) from the network rather than individual weights, which reduces the complexity of the network in ways that align with how computations are performed on hardware, allowing for gains in computational efficiency to be easily realized without specialized kit.
A formative work in popularizing the concept of structured pruning for model compression was the 2016 Li et al. paper “Pruning Filters for Efficient ConvNets,” where, as the title suggests, the authors pruned filters and their associated feature maps from CNNs in order to greatly improve computational efficiency, as the calculations surrounding these filters can be easily excluded by physically removing the chosen kernels from the model, directly reducing the size of the matrices and their multiplication operations without needing to worry about exploiting sparsity. The authors used a simple sum of filter weights (L1 norm) for magnitude-based pruning of the filters, demonstrating that their method could reduce inferences costs of VGG-16 and ResNet-110 by 34% and 38%, respectively, without significant degradation of accuracy.
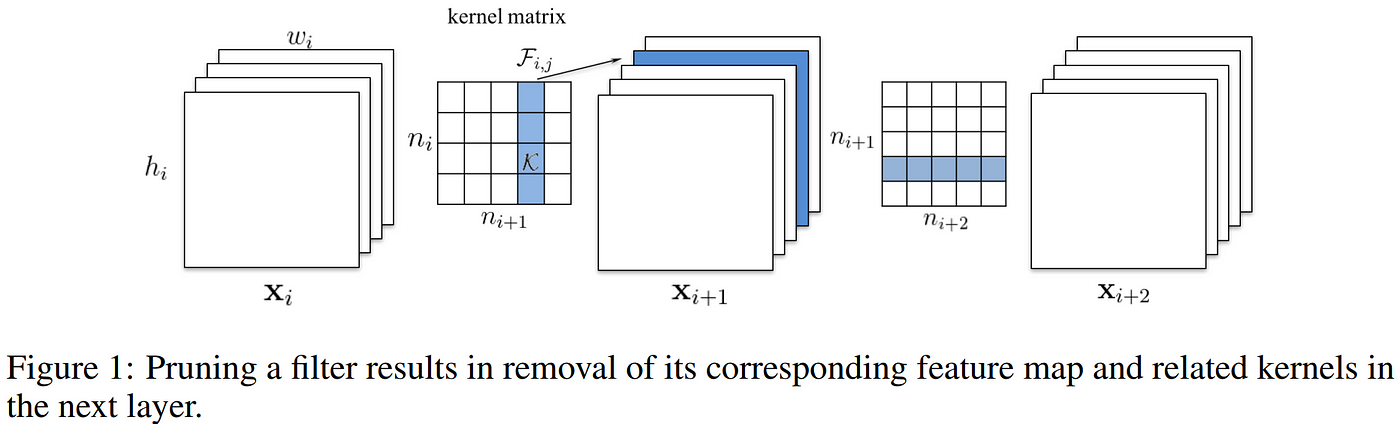
Li et al. 2016 shows the effect of pruning convolutional filters from a CNN.
Their study also reveals some fascinating insights about how convolutional networks work by comparing the sensitivity of individual CNN layers to pruning, revealing that layers on the very beginning or past halfway through the depth of the network were able to be pruned aggressively with almost no impact on the model performance, but that layers around 1/4 of the way into the network were very sensitive to pruning and doing so made recovering model performance difficult, even with retraining. The results, shown below, reveal that the layers which are most sensitive to pruning are those containing many filters with large absolute sums, supporting the theory of magnitude as a saliency measure, as these layers are clearly more important to the network, since pruning them away causes pronounced negative impact on model performance which is difficult to recover.
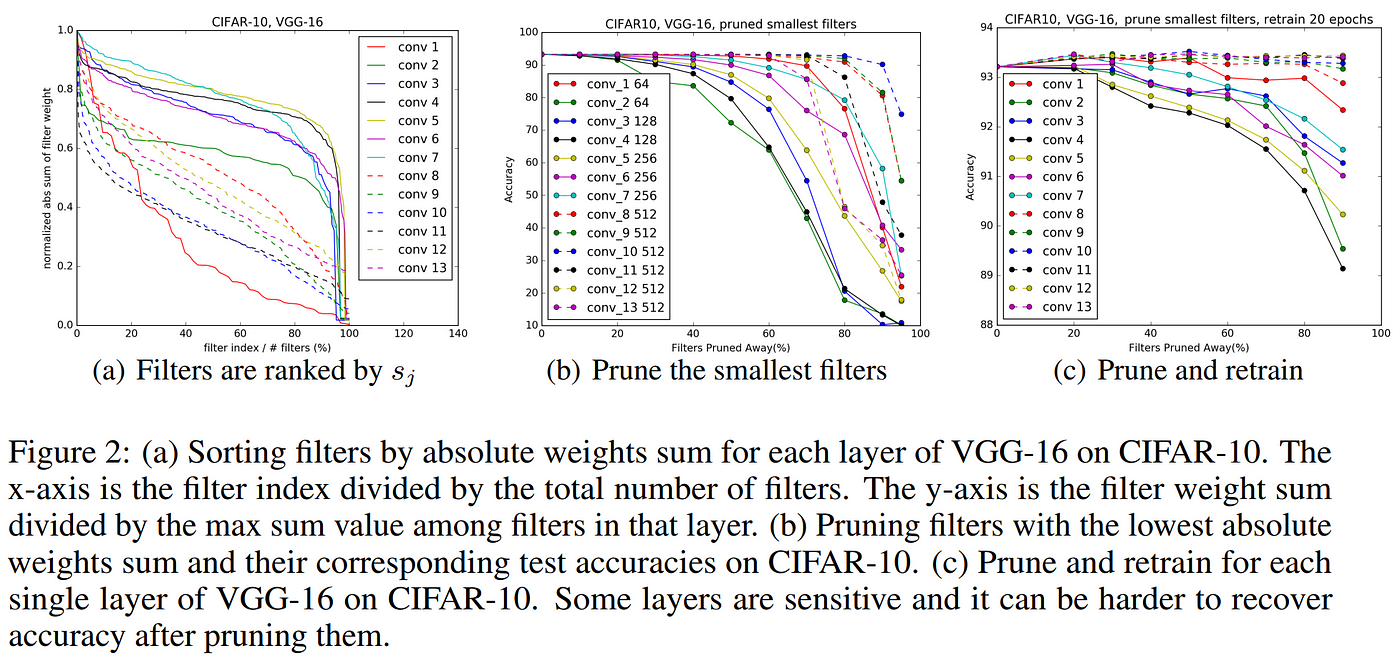
Results from Li et al. 2016 reveal marked differences in the sensitivity of CNN layers to filter pruning.
Most importantly, the results from Li et al. show that many layers in a CNN could be pruned of even up to 90% of their filters without harming (and in some cases even improving) model performance. Additionally, they found that when pruning filters from the insensitive layers, iterative retraining layer-by-layer was unnecessary, and a single round of pruning and retraining (for 1/4 of the original training time) was all that was required to recover model performance after pruning away significant portions of the network. This is great news in terms of efficiency, since multiple rounds of retraining can be costly, and previous work had reported requiring up to 3x original training time to produce their pruned models. Below we can see the overall results from Li et al. which reveal that the number of floating point operations (FLOPs) could be reduced between 15 and 40 percent in the CNNs studied without harming performance, and in fact offering gains in many instances, setting a firm example of the importance of pruning models after training.
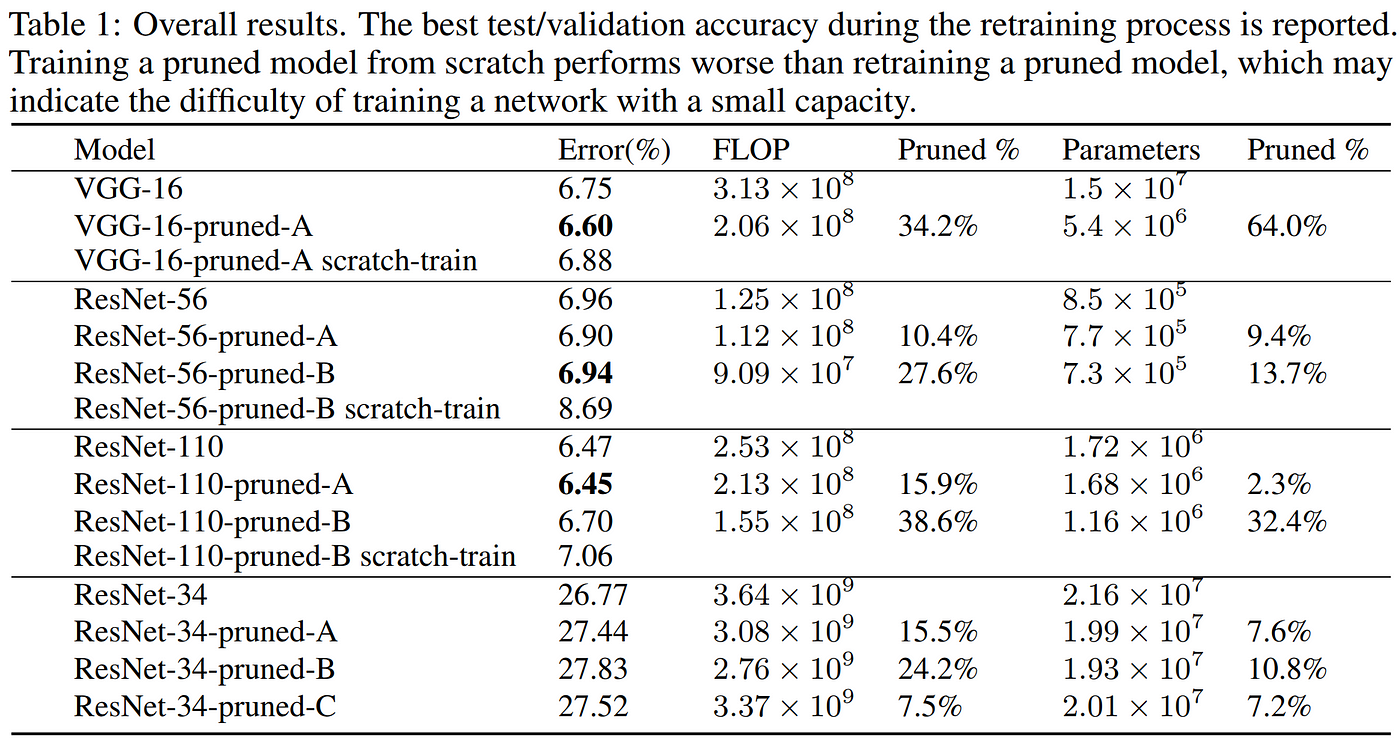
Results from Li et al. 2016 comparing their select pruning configurations to the baseline CNNs, evaluated on CIFAR-10 (top three models) and ImageNet (ResNet-34 section).
Although this study was clearly motivated by efficiency concerns, we know from decades of evidence linking reduced model complexity to improved generalization that these networks should perform better on unseen data as well, a fundamental advantage which motivated pruning research in the first place. However, this pruning method requires a sensitivity analysis of the network layers in order to be done correctly, requiring additional effort and computation. Further, as LeCun and his colleagues correctly pointed out back in 1989: although magnitude-based pruning is a time-tested strategy, we should expect a theoretically justified metric of salience to produce a superior pruning strategy, but with the size of modern neural networks, computing the Hessian matrix required for the second-order Taylor expansions used in their OBD method would be too intensive. Fortunately, a happy medium was forthcoming.
Trailing Li et al. by only a few months in late 2016, Molchanov and his colleagues at Nvidia reinvestigated the use of Taylor expansion to quantify salience for structured pruning of filters from CNNs. In contrast to OBD, they avoid the complex calculation of the second-order terms, and instead extract a useful measure of saliency by considering the variance rather than the mean of the first-order Taylor expansion term. The study provides empirical comparison of several saliency measures against an “oracle” ranking which was computed by exhaustively calculating the change in loss caused by removing each filter from a fine-tuned VGG-16. In the results shown below, we can see that the proposed Taylor expansion saliency measure most closely correlates with the oracle rankings, followed in second place by the more computationally intensive OBD, and the performance results reflect that these methods are also best at preserving accuracy, with the advantage more clearly in favor of the proposed Taylor expansion method when plotting over GFLOPs. Interestingly, the inclusion of random filter pruning in their study shows us that it performs surprisingly well compared to minimum weight (magnitude-based) pruning, challenging the notion that weight magnitude is a reliable measure of saliency, at least for the CNN architectures studied.
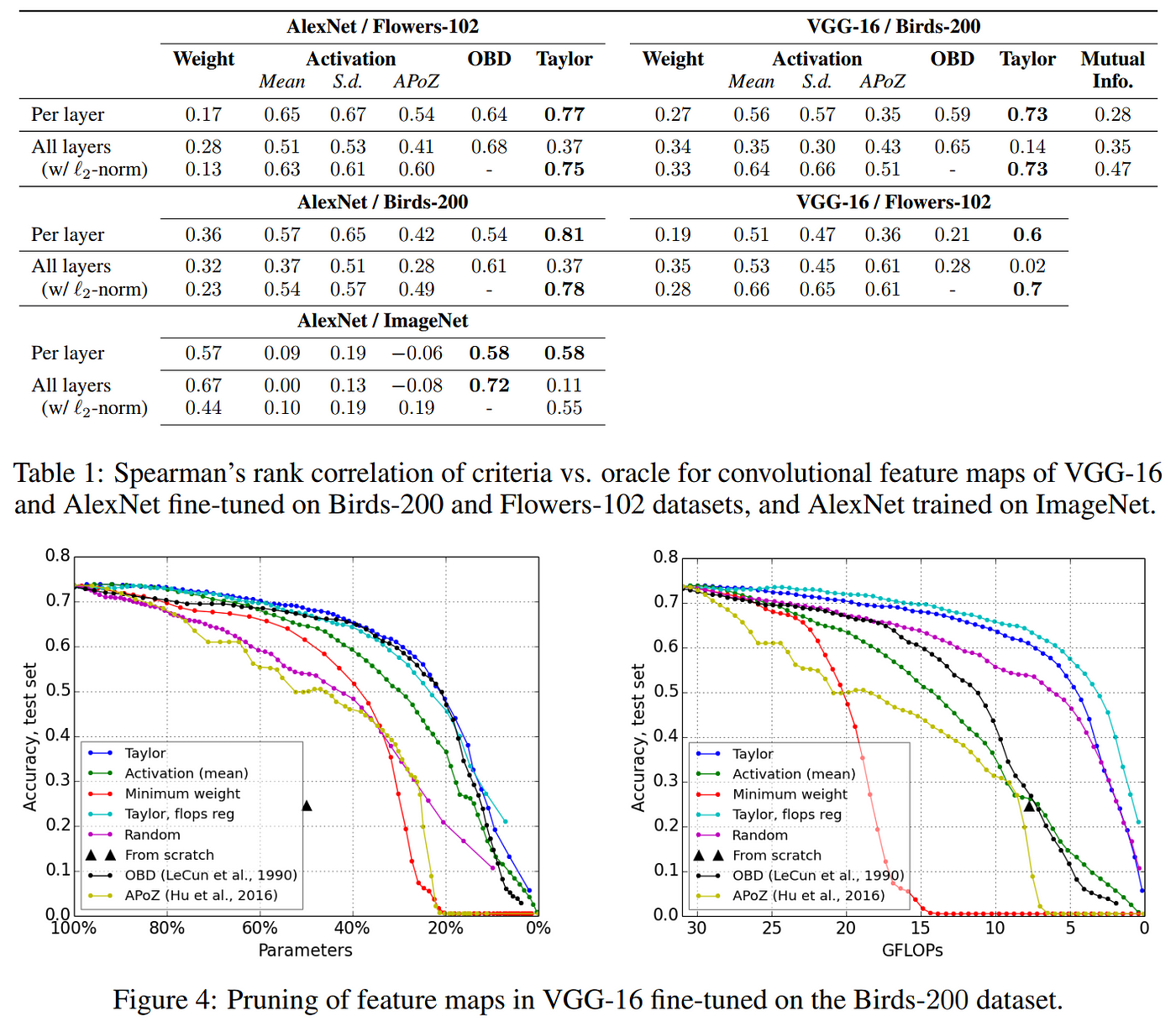
Results from Molchanov et al. 2016 show first-order Taylor expansion providing effective measure of filter saliency, representing the highest correlations with oracle ranking and best preservation of accuracy.
Pruning LLMs

Image by author using DALL-E 3.
After the widespread adoption of LLMs, researchers naturally moved to investigate the use of pruning on these architectures. Both unstructured and structured pruning can be successfully applied to LLMs to reduce their model size substantially with negligible drops in performance. As one might expect, however, the enormous size of these models requires special considerations to be made, since calculating saliency measures over models containing tens or hundreds of billions of weights is very costly, and retraining to recover model performance after pruning is prohibitively expensive. Thus, there is newfound motivation to perform pruning with as little retraining as possible, and to enforce simplicity in the saliency measures used for pruning.
Consistent with the previous eras of pruning research, it is apparent that LLMs can be pruned far more aggressively using unstructured as opposed to structured methods, but again the efficiency gains are more directly accessible with the latter. For practitioners with better access to specialized resources, exploiting the sparse matrices and massive compression rates provided by unstructured pruning may be the right choice, but for many people, the accessible efficiency gains on general hardware offered by structured pruning will be more appealing, despite the more modest levels of compression. In this section, we will review both approaches in today’s LLM landscape, so that we are equipped to make the best choice given our individual circumstances.
Unstructured Pruning of LLMs
In early 2023, SparseGPT was the first work to investigate unstructured pruning of GPT models with billions of parameters, proposing an efficient method using a novel approximate sparse regression solver to determine the prunable weights in models of this scale within a matter of hours, and demonstrating that the largest open source models of the day (≤175B) could be pruned to between 50% and 60% sparsity with minimal loss of accuracy in one shot without any retraining at all, significantly exceeding the results offered by magnitude-based approaches in the one-shot setting. Their approach takes an iterative perspective on OBS, finding that the same mathematical result can be broken down into a series of operations which are more efficient to compute. However, since their method is still an example of unstructured pruning, specialized hardware is necessary for realizing efficiency gains from their technique, and enforcing the required 2:4 or 4:8 semi-structured sparsity pattern expectation causes drops in performance compared to purely unstructured pruning.
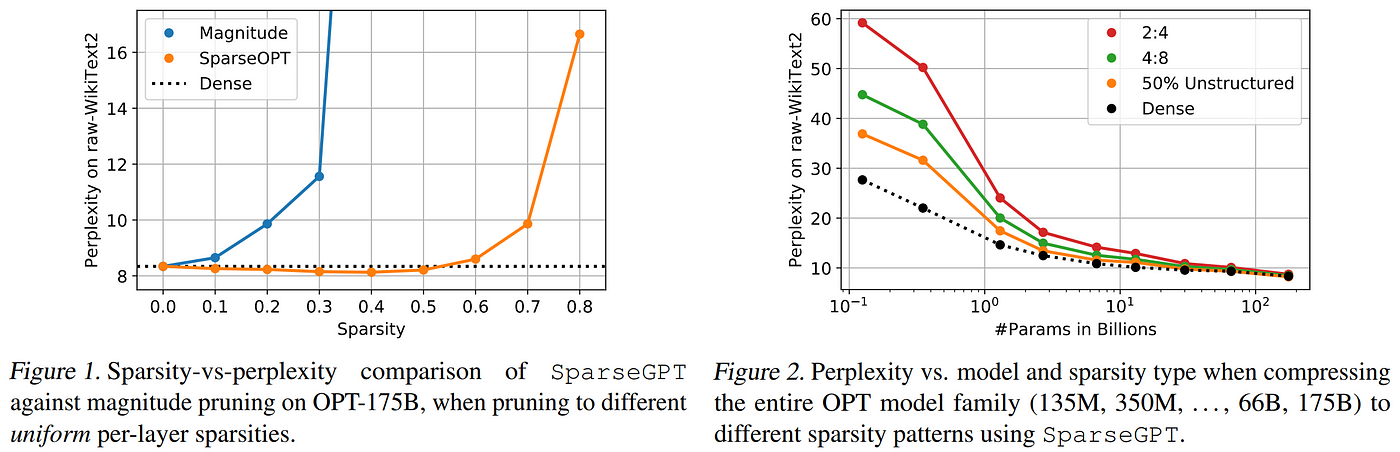
Results from SparseGPT show clear advantage over magnitude based pruning (left), and demonstrate the detrimental effects of enforcing sparsity patterns to enable hardware optimization (right).
Later in mid-2023, the authors of Wanda postulated about why quantization had seen so much more research interest than pruning in the LLM era, whereas previously the two compression techniques were equally popular. They attributed this to the fact that up until SparseGPT, all pruning methods required retraining the LLM at some point, making them cost-prohibitive to anyone without the resources to do so, creating a significant deterrent to both research and practical adoption. While SparseGPT showed that one-shot pruning was possible, their iterative OBS approach is still quite computationally intensive. In this light, Wanda opts for a simple magnitude-based unstructured pruning method, which they augment by multiplying the weight magnitudes by the norm of their associated input activations creating a more descriptive and wholistic magnitude-based measure of saliency. The comparison chart below shows the saliency formulations and complexities of these unstructured approaches.

Table from Sun et al. 2023 compares unstructured pruning approaches for LLMs and their complexity.
Wanda’s approach also produces pruned models that are ready to use without any retraining, but as an unstructured approach, again requires special hardware for efficiency gains. Nevertheless, for those equipped to take advantage of unstructured pruning, Wanda’s approach matches or exceeds the results of SparseGPT while reducing complexity by an entire factor of the model’s hidden dimension, establishing it as a strong choice for the compression of LLMs.
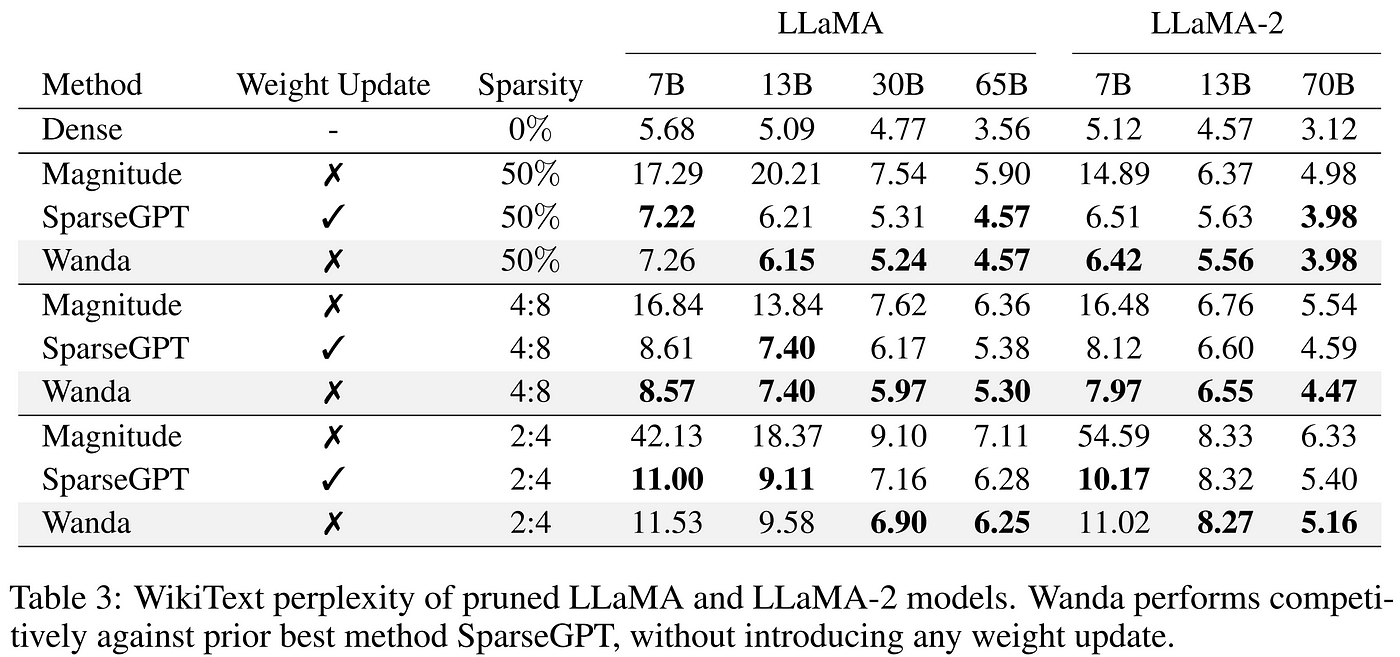
Table from Sun et al. 2023 shows competitive performance with SparseGPT with a fraction of the complexity.
Structured Pruning of LLMs
Contemporaneously with Wanda, researchers at the National University of Singapore offered a structured pruning method called LLM-Pruner. In their study, they found it necessary to settle for a 20% pruning rate, since more aggressive pruning led to substantially degraded performance. Also, while it was necessary to retrain the weights after pruning to recover model performance, they were able to achieve this using low-rank adaptation (LoRA) in just 3 hours on 50k training samples. Although the efficiency of fine-tuning with LoRA is a relief, their method nonetheless requires gradients for the full model to be generated to measure parameter saliency before pruning, so while resource-constrained users may enjoy the pruned model, performing the operation themselves may not be possible.
Just slightly later in 2023, LoRAPrune improved on the effectiveness for structured pruning of LLMs substantially by using the gradients and weights of LoRA training to establish parameter importance in the larger network, and performing iterative rounds of pruning on both the network and corresponding LoRA weights. This method is able to prune the LLaMA-65B model on a single 80GB A100 GPU, thanks to depending on the gradients of the efficient low-rank parameter space rather than the full model. Since the LLM weights remain frozen during the process, they can be quantized to 8-bit to save memory with minimal impact on the results.
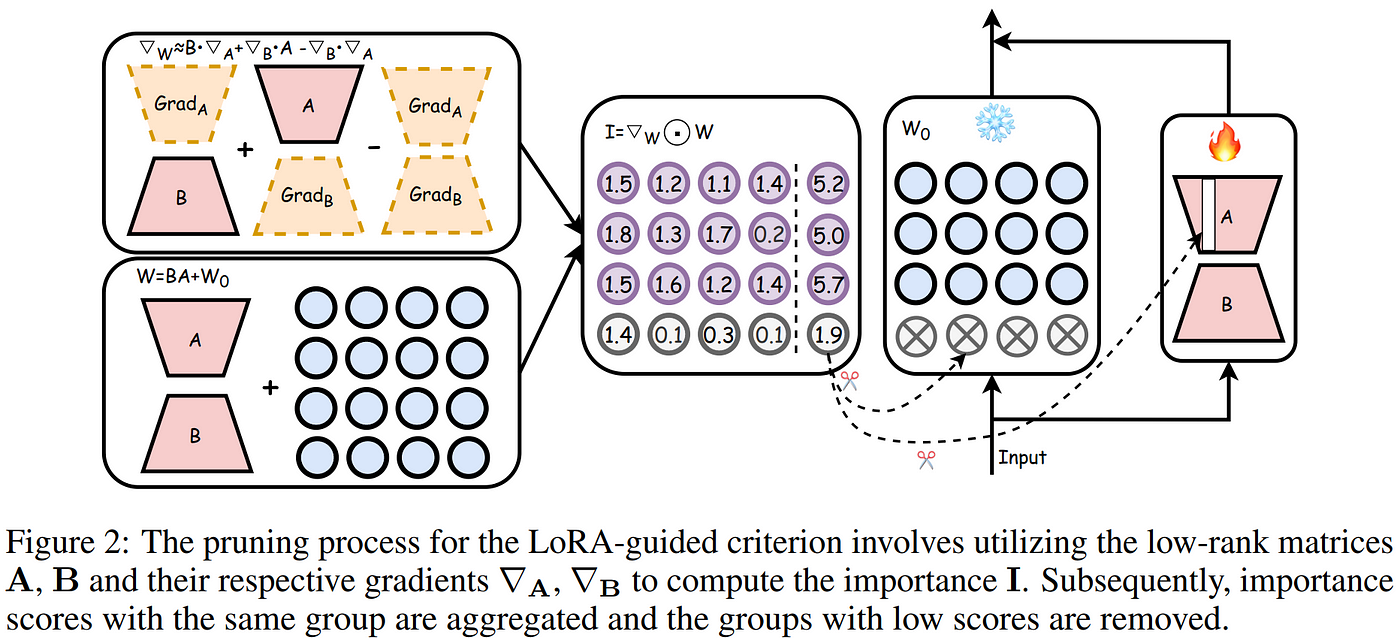
Helpful graphic from Zhang et al. 2023 depicts the structured pruning method used in LoRAPrune.
Although they came up against the same sensitivity of the LLM to more aggressive levels of structured pruning, the authors of LoRAPrune demonstrate through extensive experimentation that their method produced pruned models with superior performance compared to previous structured methods using only a fraction of the resources to perform the pruning operation.
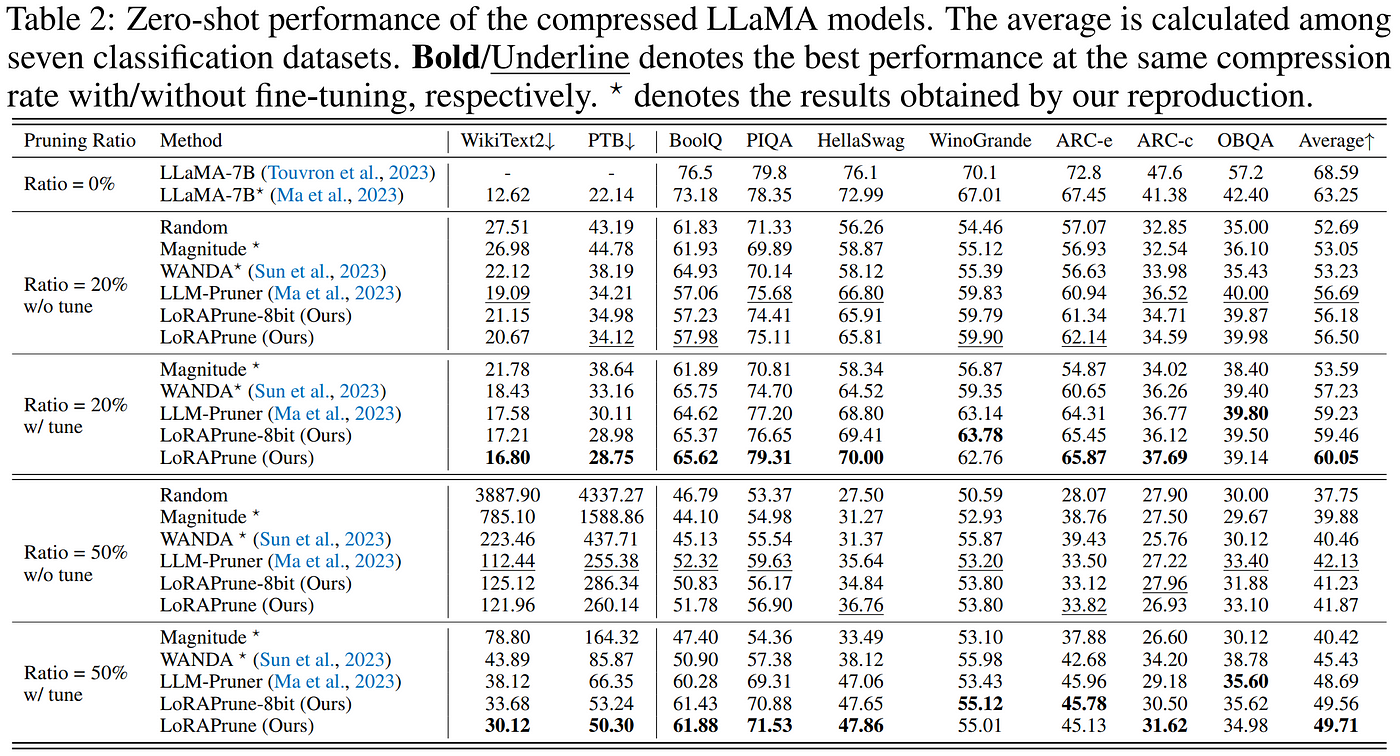
Results from LoRAPrune demonstrate a clear advantage after fine-tuning compared with previous methods.
In October of 2023, researchers at Microsoft proposed LoRAShear, a structured pruning method which uses Dependency Graph Analysis on the LLM and progressive structured pruning via LoRA Half-Space Projected Gradient (LHSPG), which “transfers the knowledge stored in the relatively redundant structures to the important structures to better preserve the knowledge of the pretrained LLM.” Additionally, they go beyond the trend in previous works of performing only instruction-based fine-tuning to recover knowledge, and instead first adaptively create a subset from the pretraining datasets based on the resulting performance distribution to recover the general pretraining knowledge that was lost during pruning, and then proceeding to “perform the usual instructed finetuning to recover domain-specific expertise and the instruction capacity of pruned LLMs.” With their more involved approach, they achieve a mere 1% drop in performance at the 20% pruning rate, and maintain an unprecedented 82% of original performance at the 50% pruning rate.
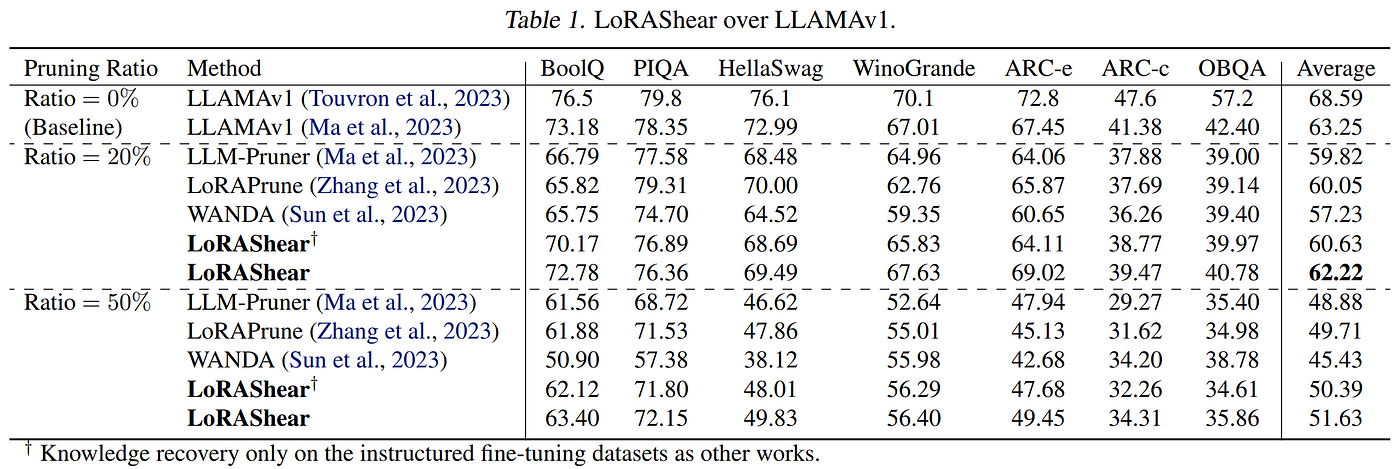
Results from LoRAShear shows superior performance, albeit with a much more complex pruning algorithm.
Then in early 2024, the aptly named Bonsai demonstrated a superior method for structured pruning of LLMs using only forward pass information, drastically reducing the computational requirements for performing the pruning process by not requiring gradients, thereby empowering those most in need of pruned models to generate them within their resource-constrained environments. With their efficient approach, they are able to closely match the performance of LoRAShear in the instruction-tuned only condition, although it would appear the additional considerations made by LoRAShear do pay dividends in knowledge recovery, but the differing spreads of evaluation datasets used in the two studies unfortunately disallow for clear comparison. Interestingly, LoRAShear is unmentioned in the Bonsai paper, presumably for the reason that the additional levels of complexity in the former make for a muddy comparison with the more straightforward methods examined by the latter, but we are left to speculate. Nevertheless, Bonsai contributes a powerful and valuable step towards democratizing LLMs and their pruning by focusing on simplicity and efficiency, able to perform the pruning operation using only the amount of GPU memory needed to run inference for a given model, and achieves impressive results with the most accessible method of structured LLM pruning published so far.

Results from Dery et al. show Bonsai achieves superior performance to previous structured pruning methods.
Conclusion

Image by author using DALL-E 3.
In this article, we’ve journeyed through the history of network pruning, starting with the dawn of unstructured techniques in the late 1980s to the current trends in LLM applications. We’ve seen that pruning is broadly categorized as either unstructured or structured pruning, depending on whether the weights are considered individually or in groups, and that the latter, while only usable at lower compression rates, provides direct relief in computational burden. We saw that gains in efficiency can be realized in the unstructured setting, but only when special storage techniques and hardware are used, and that an additional “semi-structured” condition must be obeyed for the hardware acceleration to work, which comes at a cost in performance compared with pure unstructured pruning. Pure unstructured pruning provides the most stunning compression rates with no loss in accuracy, but the irregular sparsity created does not provide efficiency gains outside of storage size, making it less appealing in the context of democratizing LLMs.
We’ve explored the concept of saliency, which refers to the various measures of importance (saliency) by which model parameters can be pruned. The most simple and accessible estimation of saliency is weight magnitude, where weights closer to zero are assumed to be less important. Although this approach is not theoretically sound (as near-zero weights can indeed be important to model performance), it is still extremely effective, and the lack of complex calculations gives it persisting popularity. On the other hand, theoretically sound measures of saliency date back to the earliest days of trainable neural networks, and are proven to produce superior models compared to magnitude-based pruning, but the complex calculations required by these early methods don’t scale well to the size of today’s LLMs. Fortunately, motivated researchers in the modern era have found ways to calculate these saliency metrics more efficiently, but alas, they still require the calculation of the gradients. In the most recent work from 2024, Bonsai demonstrated that accurate pruning can be achieved without gradients, using only the information from the forward pass.
While modern pruning research is driven primarily by the interest of compressing the unwieldy sizes of today’s top performing models so that they can be deployed on reasonably sized hardware, pruning was originally motivated by the improved generalizability that results from reducing model complexity. This regularization effect is surely taking effect in pruned LLMs, which is presumably a benefit, but the actual impact of this is less studied in today’s literature. While improving model generalizability and reducing overfitting through regularization are known to be beneficial, there may be special considerations which need to be made in the context of LLMs, which are often expected to recall minute details in vast sums of training data, depending on the use case. Therefore, it would be fruitful for future work to investigate at what point this regularization starts to have deleterious effects on intended use cases of LLMs.

